Question

CP and Cd are conjugate diameters of the ellipse; \[\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}\]; prove that the locus of the orthocentre of the triangle CPD is the curve \[2{{\left( {{b}^{2}}{{y}^{2}}+{{a}^{2}}{{x}^{2}} \right)}^{3}}=\left( {{a}^{2}}-{{b}^{2}} \right)\left( {{b}^{2}}{{y}^{2}}-{{a}^{2}}{{x}^{2}} \right)\].

Answer 1

Hint: Use concept of conjugate diameter i.e. difference between angle of two points on conjugate diameter is \[\pm \dfrac{\pi }{2}\]. Suppose parametric coordinates of P and D then proceed.

Complete step-by-step answer:
We have given ellipse; \[\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1-(1)\]
Here, we need to assume points of conjugate diameters.
Let \[\varphi \] be the eccentric angle of point P, then coordinates of P = \[\left( a\cos \varphi ,b\sin \varphi \right)\]

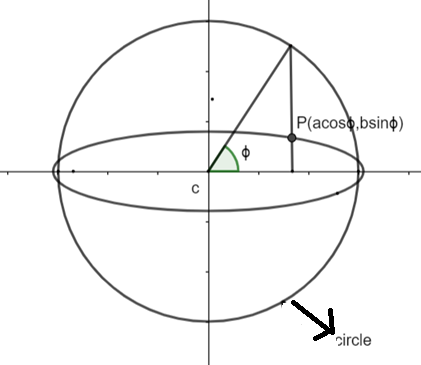
Eccentric Angle is the angle between the major axis and line joining to a circle at a point where perpendicular from any point to the major axis of ellipse is extended to circle as shown in diagram.
Since CP and CD are conjugate diameters. Hence, tangent at P is parallel to CD as per the definition of conjugate diameter.
Imp points: -
1. We need to know the relation between two conjugate diameters i.e. If \[\left( a\cos \theta ,b\sin \theta \right)\] be the coordinates of the extremity of a diameter, then \[\left( -a\sin \theta ,b\cos \theta \right)\] will be the coordinates of the extremity of its conjugate.
It means \[\theta -\varphi =\pm \dfrac{\pi }{2}\]
If \[\theta \] is an eccentric angle for eccentricity of a diameter and \[\varphi \] is eccentric angle of extremity of other diameter.
Hence, \[\vartriangle CPD\]can be represented as

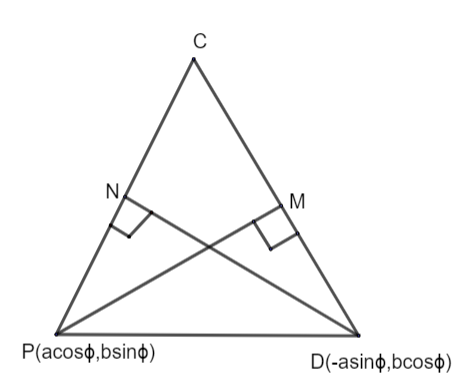
Since, C, P, D are on a circle and \[PM\bot CD\], where CD is parallel to the tangent at point P. Hence, PM is normal at point P.
Similarly, DN is normal to point D.
Hence, equation of both normals PM and DN respectively are: -
\[ax\sec \varphi -by\cos ec\varphi ={{a}^{2}}-{{b}^{2}}-(2)\]
2. (Standard formula for normal through \[a\sin \varphi ,b\cos \varphi \])
\[-ax\cos ec\varphi -by\sec \varphi ={{a}^{2}}-{{b}^{2}}-(3)\]
The locus of the orthocentre of \[\vartriangle CPD\]is obtained by eliminating \[\varphi \]between (2) and (3).
Apply cross multiplication in following manner: -
\[\dfrac{\sec \varphi }{\left( by-ax \right)\left( {{a}^{2}}-{{b}^{2}} \right)}=\dfrac{\cos ec\varphi }{\left( by+ax \right)\left( {{a}^{2}}-{{b}^{2}} \right)}=\dfrac{-1}{\left( {{b}^{2}}{{y}^{2}}+{{a}^{2}}{{x}^{2}} \right)}\]
From the above equation we can unite.
\[\begin{align}
  & \sec \varphi =\dfrac{\left( by-ax \right)\left( {{a}^{2}}-{{b}^{2}} \right)}{-\left( {{b}^{2}}{{y}^{2}}+{{a}^{2}}{{x}^{2}} \right)} \\
 & \cos ec\varphi =\dfrac{\left( by+ax \right)\left( {{a}^{2}}-{{b}^{2}} \right)}{-\left( {{b}^{2}}{{y}^{2}}+{{a}^{2}}{{x}^{2}} \right)} \\
\end{align}\]
As we know the relation \[{{\sin }^{2}}\varphi +{{\cos }^{2}}\varphi =1\]
\[\begin{align}
  & 1=\dfrac{{{\left( {{b}^{2}}{{y}^{2}}+{{a}^{2}}{{x}^{2}} \right)}^{2}}}{{{\left( by-ax \right)}^{2}}{{\left( {{a}^{2}}-{{b}^{2}} \right)}^{2}}}+\dfrac{{{\left( {{b}^{2}}{{y}^{2}}+{{a}^{2}}{{x}^{2}} \right)}^{2}}}{{{\left( by+ax \right)}^{2}}{{\left( {{a}^{2}}-{{b}^{2}} \right)}^{2}}} \\
 & \dfrac{{{\left( {{b}^{2}}{{y}^{2}}+{{a}^{2}}{{x}^{2}} \right)}^{2}}}{{{\left( by+ax \right)}^{2}}{{\left( {{a}^{2}}-{{b}^{2}} \right)}^{2}}}\left( \dfrac{1}{{{\left( by-ax \right)}^{2}}}+\dfrac{1}{{{\left( by+ax \right)}^{2}}} \right)=1 \\
 & \dfrac{{{\left( {{b}^{2}}{{y}^{2}}+{{a}^{2}}{{x}^{2}} \right)}^{2}}}{{{\left( {{a}^{2}}-{{b}^{2}} \right)}^{2}}}\times \dfrac{{{\left( by-ax \right)}^{2}}+{{\left( by+ax \right)}^{2}}}{{{\left( {{b}^{2}}{{y}^{2}}-{{a}^{2}}{{x}^{2}} \right)}^{2}}}=1 \\
 & 2{{\left( {{b}^{2}}{{y}^{2}}+{{a}^{2}}{{x}^{2}} \right)}^{3}}={{\left( {{a}^{2}}-{{b}^{2}} \right)}^{2}}{{\left( {{b}^{2}}{{y}^{2}}-{{a}^{2}}{{x}^{2}} \right)}^{2}} \\
\end{align}\]
Hence, proved.

Note: Calculation part is the most important point to take care of.
Need to remember the definition of the term auxiliary circle and how to unite polar with the help of poles. Direct formulas will take less time and are more flexible.