Question

Why is cross product not commutative?

Answer 1

Hint: The cross product is defined for two vectors. For showing that it is not communicative, we have to consider two vectors $a$ and $b$, the angle between which is $\theta $. Then we need to evaluate the cross products $a\times b$ and $b\times a$. The magnitude of the cross product of two vectors is given by $\left| a\times b \right|=\left| a \right|\left| b \right|\sin \theta $. And the direction is given by the right hand thumb rule.

Complete step by step solution:
Let us consider two vectors $a$ and $b$. Let there be an angle of $\theta $ between them, as shown in the below figure.

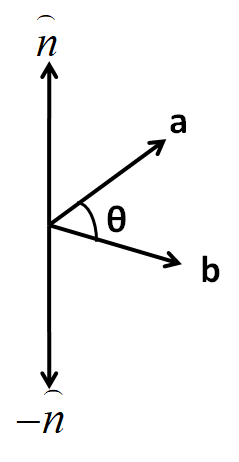
The magnitude of the cross product between the two vectors $a$ and $b$, as we know, is defined as
$\Rightarrow \left| a\times b \right|=\left| a \right|\left| b \right|\sin \theta .......\left( i \right)$
And the direction of the cross product vector is in a direction perpendicular to the plane formed by the two vectors $a$ and $b$. Now, as we can see in the above figure, there are two perpendicular directions possible, one is upwards, labeled as \[\overset\frown{n}\] and the other is downwards, labeled as $-\overset\frown{n}$. For this, we have the right hand thumb rule which is stated as below
If we turn the fingers of our right hand in a direction directed from the first vector $a$ to the second vector $b$, then our thumb will point in the direction of the cross product $a\times b$.
By using the above right hand thumb rule in the above figure, we get the direction of the cross product $a\times b$ in the vertically upward direction, \[\overset\frown{n}\]. Therefore the cross product $a\times b$ can be given as
\[\Rightarrow a\times b=\left| a \right|\left| b \right|\sin \theta \overset\frown{n}.......\left( ii \right)\]
Now, if we consider the cross product $b\times a$, then we get its magnitude by replacing $a$ by $b$, and $b$ by $a$ in (i) as
$\begin{align}
  & \Rightarrow \left| b\times a \right|=\left| b \right|\left| a \right|\sin \theta \\
 & \Rightarrow \left| b\times a \right|=\left| a \right|\left| b \right|\sin \theta \\
\end{align}$
For the direction of $b\times a$, we turn the fingers of our right hand from $b$ to $a$. Since the thumb points in the vertically downwards direction, we get the direction of the cross product $b\times a$ along $-\overset\frown{n}$. So the cross product $b\times a$ can be given by
\[\Rightarrow b\times a=\left| a \right|\left| b \right|\sin \theta \left( -\overset\frown{n} \right).......\left( iii \right)\]
From (i) and (ii) we can say that
$\Rightarrow a\times b=-\left( b\times a \right)$
From the above equation, we can conclude that the cross product is not communicative.

Note: Since the cross product of the two vectors has both the direction and the magnitude, it is also known as the vector product. We must note that only the direction of the vectors $a\times b$ and $b\times a$ are different, while the magnitudes of the two are equal. The opposite directions of the two vectors make the cross product non-communicative.