Question

How many cubes are needed to make the solid?

Answer 1

Hint: This problem can be solved by visual and mental processing. Count the number of cubes in the first layer and the same number of cubes will be there in the next layers.


Complete step-by-step answer:
The figure of the solid which made up of number of cubes is shown below,

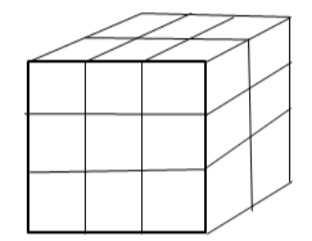
let's assume the number of cubes present in the solid be x
If we analyze the first layer of the cube. There are 3 cubes visible from the front. And there will be three cubes at the back. So total cubes in one layer is given by
$
  n = 3 + 3 \\
  n = 6 \\
 $
If we analyze the second layer of the cube. There are 3 cubes visible from the front. And there will be three cubes at the back. So total cubes in one layer is given by
$
  m = 3 + 3 \\
  m = 6 \\
$
Similarly, if we analyze the third layer of the cube. There are 3 cubes visible from the front. And there will be three cubes at the back. So total cubes in one layer is given by
$
  o = 3 + 3 \\
  o = 6 \\
 $
Thus the total number of cubes that will make up the whole solid figure is given by,
$
  x = m + n + o \\
  x = 6 + 6 + 6 \\
  x = 18 \\
 $


Note: The analysis of the solid from the front shows that 6 cubes are visible.
As one layer of the cube is also present at the back and the solid is symmetrical. Therefore, the same number of cubes will be present at the back also.
Thus, 6 cubes are at the back. So the total number of cubes required to make the solid is $6 + 6 = 12$.