Question

D and E are points on the sides CA and CB respectively of a triangle ABC right angled at C.
Prove that: $A{E^2} + B{D^2} = A{B^2} + D{E^2}$

Answer 1

Hint: Apply Pythagoras theorem here while solving.

Pictorial representation of the given problem is shown below.

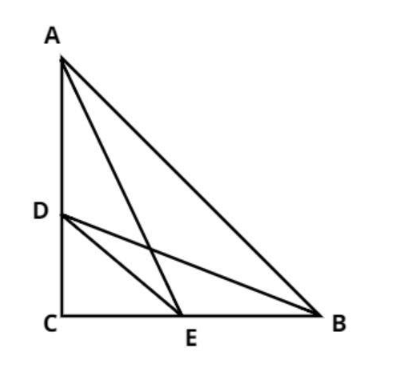
Two points D and E are on the sides AC and AB.
We have to prove $A{E^2} + B{D^2} = A{B^2} + D{E^2}$
Join the point D with B and E and the point E with A.
Proof: -
Using Pythagoras Theorem,
We know that
${\text{Hypotenuse}}{{\text{e}}^2} = {\text{Perpendicular}}{{\text{r}}^2} + {\text{Bas}}{{\text{e}}^2}$
In $\Delta ACE,$
 $A{E^2} = A{C^2} + C{E^2}.........\left( 1 \right)$
In $\Delta BCD,$
 $B{D^2} = D{C^2} + B{C^2}.........\left( 2 \right)$
In $\Delta ABC,$
 $A{B^2} = A{C^2} + B{C^2}.........\left( 3 \right)$
In $\Delta DCE,$
 $D{E^2} = D{C^2} + C{E^2}.........\left( 4 \right)$
Now, consider L.H.S which is$A{E^2} + B{D^2}$
From equation (1) and (2)
$A{E^2} + B{D^2} = A{C^2} + C{E^2} + D{C^2} + B{C^2}.........\left( 5 \right)$
Now, consider R.H.S which is$A{B^2} + D{E^2}$
From equation (3) and (4)
$A{B^2} + D{E^2} = A{C^2} + B{C^2} + D{C^2} + C{E^2}.........\left( 6 \right)$
Now from equation (5) and (6) it is clear that L.H.S = R.H.S
Therefore $A{E^2} + B{D^2} = A{B^2} + D{E^2}$
Hence Proved.

Note:In such types of questions first draw the pictorial representation of the given problem then, apply Pythagoras Theorem in all different right angle triangles which is right angled at C, then find out the value of L.H.S and R.H.S separately, then we see that both are equal which is the required result.