Question

Define a feasible region in LPP.

Answer 1

Hint: In this question, we have to define feasible regions in linear programming problems. For this, we will first understand the meaning of feasible regions in LPP and then take an example to determine the feasible region of the linear programming problem. Using all this, we will finally give a definition of a feasible region in LPP.

Complete step-by-step solution
Let us understand linear programming problems and then understand feasible regions.
The process of finding the optimal levels with the system of linear inequalities is called linear programming.
To solve the given linear programming problem, linear inequalities are drawn on graphs and the inequality $\left( \le,\ge \right)$ tells us the region, which particular linear inequality will cover. When all linear inequalities are drawn on a graph, the common region for all of them represents a feasible region. This feasible region gives us an optimal value of the given LPP. Let us take an example to understand feasible regions clearly.
For example: Constraints are given as:
$x\ge 0,y\ge 0,x+y\le 6,y\le x+3$.
For this let us draw a graph,
For inequality the $x+y\le 6$ line will be drawn according to x+y=6 and the region will be considered below the line towards the origin. Coordinates at the x and y-axis can be found as,
\[\begin{align}
  & \Rightarrow x=0,0+y=6\Rightarrow y=6\Rightarrow \left( 0,6 \right) \\
 & \Rightarrow y=0,x+0=6\Rightarrow x=6\Rightarrow \left( 6,0 \right) \\
\end{align}\]
For inequality $y\le x+3$ it can be written as $y-x\le 3$. The line will be drawn according to y-x=3 and the region will be considered below the line towards the origin. Coordinates at the x and y-axis can be found as,
\[\begin{align}
  & \Rightarrow x=0,y-0=3\Rightarrow y=3\Rightarrow \left( 0,3 \right) \\
 & \Rightarrow y=0,0-x=3\Rightarrow x=-3\Rightarrow \left( -3,0 \right) \\
\end{align}\]
Also, we will take the region in the positive quadrant because $x\ge 0\text{ and }y\ge 0$. So, the graph becomes

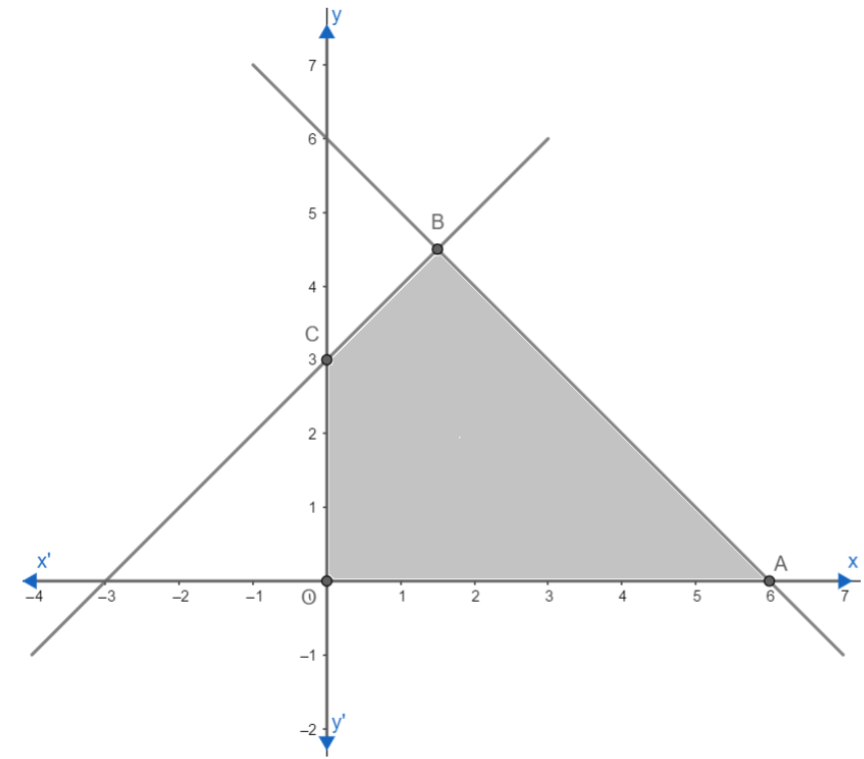
The region formed by all constraints in the region OABC which is our feasible region. The set of points enclosed in this region will give us an optimal solution for an LPP. So now let us define feasible regions in LPP.
A feasible region is an area defined as a set of coordinates that satisfy a system of inequalities. This region satisfies all the restrictions imposed by a linear programming scenario.

Note: Students should note that some linear programming problems do not have any feasible region. Sometimes different constraints form different areas, which are not common and thus cannot be considered as feasible regions. We have to consider every constraint to find the required feasible region in the LPP.