
Define a modulus function. Find its domain and range. Also draw its graph.
Answer
570k+ views
Hint: First of all, before proceeding to the topic we have to know what function is. And after that we have to know what modulus is. After learning these two topics, we have to proceed for the modulus function and later on its properties. A modulus function when opened will have both positive and negative values for that function.
Complete step by step answer:
So, now before proceeding to the modulus function let us discuss the Function and Modulus in general.
Let us understand the concept of functions by using simple examples:
1. The area of the Circle can be represented as \[A=\pi {{r}^{2}}\] in terms of radius. The area \[A\] depends on radius \[r\]. In general terms, we can say that \[A\] is a function of \[r\].
2. Similarly volume \[V\] is also a function of its radius \[r\]. It can be represented as \[V=\dfrac{4}{3}\pi {{r}^{3}}\].
Definition (Modulus): The modulus value of a real number \[x\] can be denoted by \[\left| x \right|\], it denotes the non-negative value of \[x\] without depending on the sign. It is also called Absolute Value.
Now, we can define modulus function as \[f(x)=\left| x \right|\].
Now, if \[x\] is non-negative or positive, then the output of \[f\] will be \[x\].
If \[x\] is negative, then the output of \[f\] will be \[-x\], it can be represented as shown below
\[f(x)=\left\{ \begin{matrix}
x & \text{if }x\ge 0 \\
-x & \text{if }x < 0 \\
\end{matrix} \right.\] ……. (1)
Domain and Range of the modulus function:
Before proceeding to find the domain and range of the modulus function, we have to know what domain and range is.
Definition (Domain): In general form the Domain can be defined as the values that are getting into the function. i.e. the inputs are said to be in Domain.
Definition (Range): In general form the Range can be defined as the values are coming out of the function. i.e. the outputs are said to be in Range.
Since we are applying this modulus function on real numbers, the domain will be \[\mathbb{R}\], and the range is the set of non-negative integers or we can say the interval \[\left[ 0,\infty \right)\].
The graph of the modulus function can be drawn as shown below:
First we have to construct a table of points, so that we can draw the graph easily.
The values of \[f(x)\] can be obtained by substituting the values of \[x\] in equation (1).
Now the graph can be drawn as shown in the figure below.
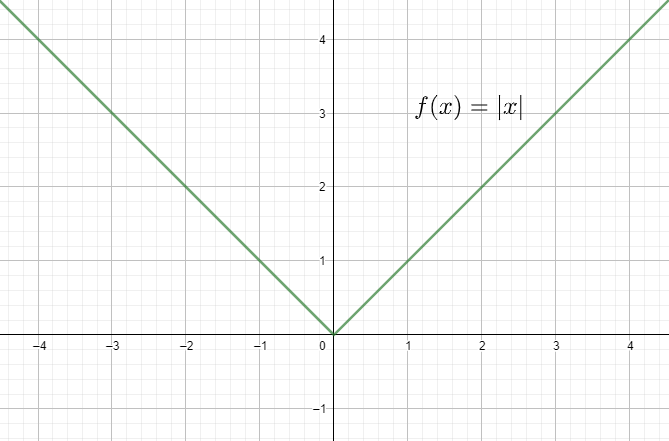
Note: Students may have the chances to make mistakes while taking the values of \[f(x)\] as it completely depends on the value of \[x\], students have to focus on the value of \[x\]. While plotting the graph, we have to consider both positive and negative values of x with same magnitudes. Only then the graph we obtain will be complete.
Complete step by step answer:
So, now before proceeding to the modulus function let us discuss the Function and Modulus in general.
Let us understand the concept of functions by using simple examples:
1. The area of the Circle can be represented as \[A=\pi {{r}^{2}}\] in terms of radius. The area \[A\] depends on radius \[r\]. In general terms, we can say that \[A\] is a function of \[r\].
2. Similarly volume \[V\] is also a function of its radius \[r\]. It can be represented as \[V=\dfrac{4}{3}\pi {{r}^{3}}\].
Definition (Modulus): The modulus value of a real number \[x\] can be denoted by \[\left| x \right|\], it denotes the non-negative value of \[x\] without depending on the sign. It is also called Absolute Value.
Now, we can define modulus function as \[f(x)=\left| x \right|\].
Now, if \[x\] is non-negative or positive, then the output of \[f\] will be \[x\].
If \[x\] is negative, then the output of \[f\] will be \[-x\], it can be represented as shown below
\[f(x)=\left\{ \begin{matrix}
x & \text{if }x\ge 0 \\
-x & \text{if }x < 0 \\
\end{matrix} \right.\] ……. (1)
Domain and Range of the modulus function:
Before proceeding to find the domain and range of the modulus function, we have to know what domain and range is.
Definition (Domain): In general form the Domain can be defined as the values that are getting into the function. i.e. the inputs are said to be in Domain.
Definition (Range): In general form the Range can be defined as the values are coming out of the function. i.e. the outputs are said to be in Range.
Since we are applying this modulus function on real numbers, the domain will be \[\mathbb{R}\], and the range is the set of non-negative integers or we can say the interval \[\left[ 0,\infty \right)\].
The graph of the modulus function can be drawn as shown below:
First we have to construct a table of points, so that we can draw the graph easily.
| \[x\] | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| \[f(x)\] | 4 | 3 | 2 | 1 | 0 | 1 | 2 | 3 | 4 |
The values of \[f(x)\] can be obtained by substituting the values of \[x\] in equation (1).
Now the graph can be drawn as shown in the figure below.

Note: Students may have the chances to make mistakes while taking the values of \[f(x)\] as it completely depends on the value of \[x\], students have to focus on the value of \[x\]. While plotting the graph, we have to consider both positive and negative values of x with same magnitudes. Only then the graph we obtain will be complete.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Trending doubts
What are the major means of transport Explain each class 12 social science CBSE

Which are the Top 10 Largest Countries of the World?

Draw a labelled sketch of the human eye class 12 physics CBSE

How much time does it take to bleed after eating p class 12 biology CBSE

Explain sex determination in humans with line diag class 12 biology CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE




