Question

Define electric field strength. Is it a vector or a scalar quantity?

Answer 1

Hint: According to Coulomb’s Law, the force between two charges is given by $F = \dfrac{{{q_1}{q_2}}}{{4\pi {\varepsilon _0}{r^2}}}$. Think of a quantity that can be used to obtain the influence of one charge on the other charge(s). The electric field can be considered in analogy with the gravitational field.

Complete step by step answer:
The force between two particles having charges ${q_1}$ and ${q_2}$, separated by a distance $r$ is given as $F = \dfrac{{{q_1}{q_2}}}{{4\pi {\varepsilon _0}{r^2}}}$. If the charges are of the same sign, the force will be repulsive.
In vector form, the force is given by $\overrightarrow F = \dfrac{{{q_1}{q_2}}}{{4\pi {\varepsilon _0}{r^2}}}\overrightarrow r $, where $\overrightarrow r $ is the relative position vector of ${q_2}$ with respect to ${q_1}$.

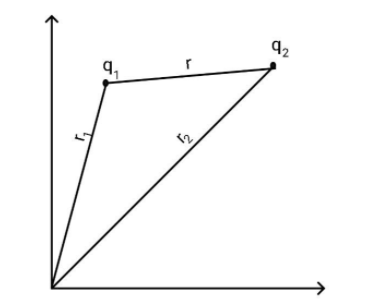
You can see that the direction of the force is along the relative position vector. This can be considered as an influence on one charge by the other.
Consider a single charge in space having charge $q$, this charge creates a field in the entire space. This field exerts the force which a charge will experience under the influence of the field. This field generated by the charge is known as the Electric Field.
Now consider the above charge and its generated field. Bring another charge $q'$ in the field of $q$ at a distance $r$from the source charge. The charge brought is called a test charge. Now, the force on the charge $q'$ by the field of source charge is given as $F = \dfrac{{qq'}}{{4\pi {\varepsilon _0}{r^2}}}$.
\[
 F = q'\dfrac{q}{{4\pi {\varepsilon _0}{r^2}}} \\
\Rightarrow F = q'E \\
 \therefore E = \dfrac{F}{{q'}} \\
 \]
$E$ is the electric field strength and is equal to the force applied by the field on a unit positive charge.
Since force is a vector quantity, the electric field strength is also a vector quantity.
Hence, electric field strength is defined as the force per unit charge and it is a vector quantity.

Note:
Here we have considered a single source charge. If $n$ number of charges are present, or a charge distribution is present, the net electric field at a point is given as the vector sum of the individual electric field due to charges. For discrete charge distribution, the net electric field is given as $\sum\limits_{i = 1}^n {{E_i}} $. For a continuous charge distribution, the net electric field is given as $\int {dE} $, where $dE$ is the electric field due to charge $dq$.