
Define feasible region.
Answer
529.2k+ views
1 likes
Hint: It is related to the chapter linear programming and used in the topic mathematical optimization by using the given constraints. Now, define it.
Complete step-by-step answer:
A feasible region is defined as an area bounded by a set or collection of coordinates that satisfy a system of given inequalities.
The region satisfies all restrictions imposed by a linear programming scenario.
It is a concept of an optimization technique. It means a feasible region is the set of all points whose coordinates satisfy the constraints of a problem.
Explanation:-
For example, for constraints
The feasible region is shown below which is represented by an area bounded by all above equations.
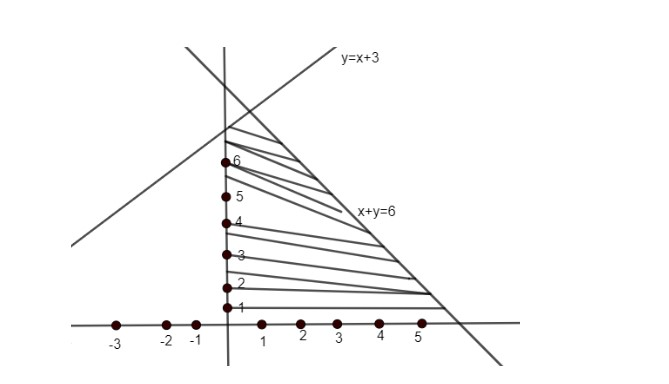
The area represented above is termed as a feasible region.
Hence, a planner can use linear programming to determine the best value obtainable under conditions dictated by several linear equations that relate to a real-life problem. So, In mathematics optimization , a feasible region is the set of all possible points of an optimization problem that satisfy problems constraints , potentially including inequalities , equalities and integer constraints.
Note: One can get confused with the similar term i.e. feasible region in mathematical optimization.
If the constraints of an optimization problem are mutually contradictory, there are no points that satisfy all the constraints and thus a feasible region has null set. In the above problem, it has a solution and is said to be feasible.
Complete step-by-step answer:
A feasible region is defined as an area bounded by a set or collection of coordinates that satisfy a system of given inequalities.
The region satisfies all restrictions imposed by a linear programming scenario.
It is a concept of an optimization technique. It means a feasible region is the set of all points whose coordinates satisfy the constraints of a problem.
Explanation:-
For example, for constraints
The feasible region is shown below which is represented by an area bounded by all above equations.

The area represented above is termed as a feasible region.
Hence, a planner can use linear programming to determine the best value obtainable under conditions dictated by several linear equations that relate to a real-life problem. So, In mathematics optimization , a feasible region is the set of all possible points of an optimization problem that satisfy problems constraints , potentially including inequalities , equalities and integer constraints.
Note: One can get confused with the similar term i.e. feasible region in mathematical optimization.
If the constraints of an optimization problem are mutually contradictory, there are no points that satisfy all the constraints and thus a feasible region has null set. In the above problem, it has a solution and is said to be feasible.
Latest Vedantu courses for you
Grade 10 | MAHARASHTRABOARD | SCHOOL | English
Vedantu 10 Maharashtra Pro Lite (2025-26)
School Full course for MAHARASHTRABOARD students
₹33,300 per year
EMI starts from ₹2,775 per month
Recently Updated Pages
Master Class 4 Maths: Engaging Questions & Answers for Success

Master Class 4 English: Engaging Questions & Answers for Success

Master Class 4 Science: Engaging Questions & Answers for Success

Class 4 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Trending doubts
Give 10 examples of unisexual and bisexual flowers

Draw a labelled sketch of the human eye class 12 physics CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Why is the cell called the structural and functional class 12 biology CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE




