Question

Define focal length of a spherical lens.

Answer 1

Hint: The distance between the optical center and the principal focus of a spherical lens is known as the Focal length of a spherical lens.

Formula used:

$\dfrac{1}{u}+\dfrac{1}{v}=\dfrac{1}{f}$

Complete step by step answer:
A spherical lens is a type of lens whose surface has the shape of the surface of a sphere. It has the same curve across its entire surface. It is easily possible to determine whether the lens is spherical or not by studying the image formed by it when two lines crossed at ${{90}^{\circ }}$, is viewed through the lens. Spherical lens would cause no distortion of the cross sign.

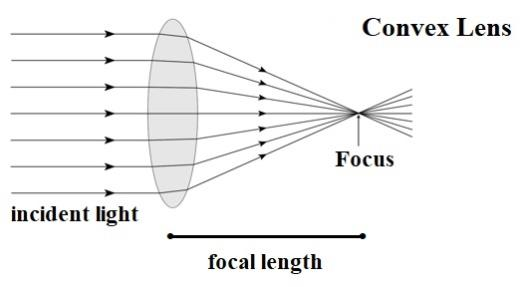
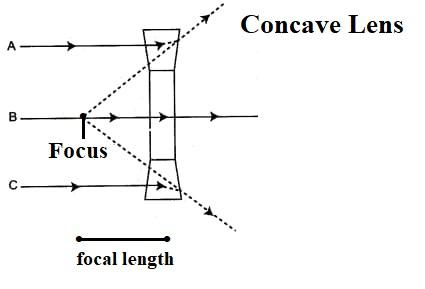
Focal length of a spherical lens is the distance between optical centre and focus of the lens. The Focal length of a lens is half of its radius of curvature. We usually denote the centre of curvature of a lens with the term $\text{2F}$instead of denoting it by C.

We can find focal length of a lens using lens formula,

$\dfrac{1}{u}+\dfrac{1}{v}=\dfrac{1}{f}$

Where $u$ is the distance of the object from the lens, $v$ is the distance of image formed from the lens, and $f$ is the focal length of the lens.

Additional information:
Important terms to know about spherical lenses:

Centre of curvature – it is the centre of the sphere of which lens is a part of convex and concave lenses have two centres of curvature, denoted by ${{\text{C}}_{\text{1}}}$and${{\text{C}}_{\text{2}}}$.

a.)Focus – It is the point at which all the parallel rays of light converge in case of convex lens and all the parallel rays of light seem to diverge from an imaginary point in case of concave lens.

b.)Principal axis – It is an imaginary line that passes through the centres of curvature of lens.

c.)Optical centre – It is the central point of a lens. A ray of light passes without deviation through the optical centre.

d.)Radius of curvature – It is the distance between optical centre and centre of curvature of a lens.

Note:
While calculating focal length of lens, always take image distance negative in both cases, convex and concave lens. For convex lenses, image distance is positive but in concave lens, image distance is taken as negative. Focal length of convex lens is positive while that of concave lens is negative.