Question

For the angle of minimum deviation of a prism to be equal to its refracting angle, the prism must be made of a material whose refractive index:
\[A)\] Lies between \[\sqrt{2}\] and \[1\].
\[B)\] Lies between \[2\] and \[\sqrt{2}\].
\[C)\] Is less than \[2\].
\[D)\] Is greater than \[2\].

Answer 1

Hint: Firstly we need to draw a diagram to understand the situation clearly. We will use the equation to find the refractive index of a prism and substitute the given situation of angle of minimum deviation in the expression and hence obtain an equation for the refractive index. Then we will apply the limit from \[0{}^\circ \] to \[90{}^\circ \] and obtain the range of refractive index which we could have using the given angle of minimum deviation.

Formula used:
\[\mu =\dfrac{\sin \dfrac{\left( A+{{\delta }_{m}} \right)}{2}}{\sin \dfrac{A}{2}}\]

Complete step by step answer:
We will draw the diagram using the parameters, angle of prism as (\[A\]), angle of incidence (\[i\]), angle of refraction (\[r\]) and angle of minimum deviation (\[{{\delta }_{m}}\]).

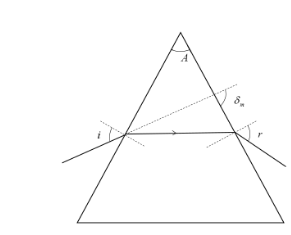
It is given that angle of minimum deviation to be equal to the refracting angle.
\[\Rightarrow {{\delta }_{m}}=A\]
Now, we will substitute this in the equation to find the refractive index of prism and it will become,
\[\mu =\dfrac{\sin \dfrac{\left( A+A \right)}{2}}{\sin \dfrac{A}{2}}=\dfrac{\sin \left( A \right)}{\sin \dfrac{A}{2}}\]
Now, we will use the trigonometric relation \[\sin \left( x \right)=2\sin \left( \dfrac{x}{2} \right)\cos \left( \dfrac{x}{2} \right)\].
\[\Rightarrow \mu =\dfrac{\sin \left( A \right)}{\sin \dfrac{A}{2}}=\dfrac{2\sin \left( \dfrac{A}{2} \right)\cos \left( \dfrac{A}{2} \right)}{\sin \left( \dfrac{A}{2} \right)}\]
\[\mu =2\cos \left( \dfrac{A}{2} \right)\]

So, we have the expression for a refractive index.
Now we will apply the limit for angle of prism from \[0{}^\circ \] to \[90{}^\circ \]. Then, if \[A\] is \[0{}^\circ \],
\[\mu =2\cos \left( \dfrac{0}{2} \right)=2\]
And if \[A\] is \[90{}^\circ \], \[\mu =2\cos \left( \dfrac{90}{2} \right)= 2\cos \left( 45 \right)=\sqrt{2}\]
So, we can conclude that the prism could have a refractive index which lies between \[2\] and \[\sqrt{2}\].

So, the correct answer is “Option B”.

Note:
The soul of this question is situated at the part where we are applying the limit for \[A\].
There we are taking the angles \[0{}^\circ \] to \[90{}^\circ \] because they are the maximum and minimum angles which a prism could have. We are taking \[{{\delta }_{m}}=A\] because if the minimum deviation is equal to refracting angle, by geometry, the angle of prism and the refracting angles will be equal.