Question

Define injective function. Give an example of injective function.

Answer 1

Hint: We solve this problem by defining the injective function and then we take some examples.
The injective function is also called as one – one function which is defined as “for every element in the codomain there is the image of exactly one element in the domain”. The graphical representation of a function \[f:X\to Y\] is as shown below.

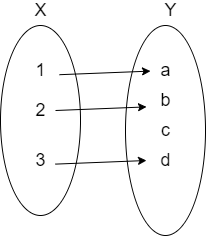
Here, X is the domain and the set Y is called the codomain.
By using this definition we take some examples of injective functions.

Complete step by step answer:
We are asked to define the injective function.
The injective function is defined as a function in which for every element in the codomain there is an image of exactly one in the domain.
Let us assume that a function mapping as \[f:X\to Y\] then the graphical representation of this function if it is injective is given as

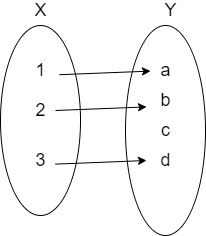
Here, we can see that for every element in the domain X there is exactly one image in the codomain Y.
So, we can say that this function is an injective function.
There is other definition of injective in mathematical form as follows:
“A function of domain X is said to an injective function if for any two elements \[a,b\] in the domain X, whenever \[f\left( a \right)=f\left( b \right)\] then \[a=b\]”
Symbolically we can say that
\[\forall a,b\in X,f\left( a \right)=f\left( b \right)\Rightarrow a=b\]
Now, let us take one example as follows
(1) The function \[f:\mathbb{R}\to \mathbb{R}\] is defined as \[f\left( x \right)=nx\] where \['n'\] is constant.
Let us check whether this function is injective or not.
Let us assume two values \[a,b\in \mathbb{R}\] such that
\[\Rightarrow f\left( a \right)=f\left( b \right)\]
Now by using the function \[f\left( x \right)=nx\] in above equation we get
\[\begin{align}
  & \Rightarrow na=nb \\
 & \Rightarrow a=b \\
\end{align}\]
We know that if a function is defined as \[\forall a,b\in X,f\left( a \right)=f\left( b \right)\Rightarrow a=b\] then we can say that the function is injective.
By using this definition we can conclude that the function \[f:\mathbb{R}\to \mathbb{R}\] is defined as \[f\left( x \right)=nx\] where \['n'\] is constant is a injective function.
Let us take some more examples of injective functions as follows:
(2) The function \[f:\mathbb{R}\to \mathbb{R}\] is defined as \[f\left( x \right)={{e}^{nx}}\] where \['n'\] is constant.
(3) The function \[f:\mathbb{R}\to \mathbb{R}\] is defined as \[f\left( x \right)={{x}^{2n+1}}\] where \['n'\] is constant.

Note: We come across some situations where we are asked to check whether a given function is injective or not. Then we use the mathematical definition in the case that is
\[\forall a,b\in X,f\left( a \right)=f\left( b \right)\Rightarrow a=b\]
But students may do from the direct definition that is “for every element in the codomain there is the image of exactly one element in the domain”
Here we need to check for each and every element in the domain.
If the function is mapped as \[f:\mathbb{R}\to \mathbb{R}\] then we need to check each and every element in the domain that is real numbers. But we have infinite real numbers then it will be impossible to check the injection from the general definition.
So, we need to use the mathematical definition for solving the problem easily.