
Define relaxation time of the free electrons drifting in a conductor: How is it related to the drift velocity of free electrons? Use this relation to deduce the expression for the electrical resistivity of the material.
Answer
440.6k+ views
Hint: Drift velocity is directly proportional to relaxation time. Write the formula for current flowing through the conductor. Substitute the value of drift velocity in terms of relaxation time. Use the formula for electric field applied and Ohm’s law. Get the value of R in terms of l and A.
Formula used:
Complete step by step answer:
Relaxation time is defined as the time interval between two successive collisions of electrons in a conductor when current flows through it. It is denoted by
Relation between drift velocity of the electrons (
Where, E: Electric field
M: mass of electron
E: charge of electron
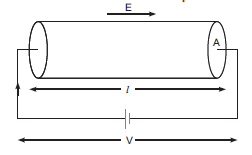
Consider a conductor having length l, area of cross section A and current density n.
Current flowing through the conductor is given by,
Now, by substituting equation.(1) in equation.(2) we get,
Electric field applied is given by,
Substituting equation. (3) in equation.(4) gives,
Now, by rearranging the equation we get,
According to Ohm’s Law,
Rearranging the above equation we get,
Now, substituting the equation. (5) in above equation we get,
Let
Where,
Therefore, the expression for electrical resistivity is given by
Note:
Electrical resistivity is inversely proportional to relaxation time. Reciprocal resistivity gives conductivity. It is denoted by
As the temperature of the conductor is decreased, the number of electron collisions also decreases. As a result, relaxation time gets increased. Thus we can say, relaxation time is dependent on temperature.
Formula used:
Complete step by step answer:
Relaxation time is defined as the time interval between two successive collisions of electrons in a conductor when current flows through it. It is denoted by
Relation between drift velocity of the electrons (
Where, E: Electric field
M: mass of electron
E: charge of electron

Consider a conductor having length l, area of cross section A and current density n.
Current flowing through the conductor is given by,
Now, by substituting equation.(1) in equation.(2) we get,
Electric field applied is given by,
Substituting equation. (3) in equation.(4) gives,
Now, by rearranging the equation we get,
According to Ohm’s Law,
Rearranging the above equation we get,
Now, substituting the equation. (5) in above equation we get,
Let
Where,
Therefore, the expression for electrical resistivity is given by
Note:
Electrical resistivity is inversely proportional to relaxation time. Reciprocal resistivity gives conductivity. It is denoted by
As the temperature of the conductor is decreased, the number of electron collisions also decreases. As a result, relaxation time gets increased. Thus we can say, relaxation time is dependent on temperature.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Class 12 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Economics: Engaging Questions & Answers for Success

Trending doubts
Draw a labelled sketch of the human eye class 12 physics CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Which one of the following is a true fish A Jellyfish class 12 biology CBSE

Why is the cell called the structural and functional class 12 biology CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Write the difference between solid liquid and gas class 12 chemistry CBSE




