Question

Define Supplementary Angles.

Answer 1

Hint: We recall the definition of the supplementary angles which is a pair of angles whose sum of measures is equal to the measure of a straight angle or $180{}^\circ $. The two supplementary angles may be subtended on a straight line or may exist separately. \[\]

Complete step-by-step answer:
We know that the measure of an angle is the amount of rotation taken in an anti-clockwise direction . Let us take two lines $AB$ and $CD$ intersect each other at the point $O.$\[\]
 

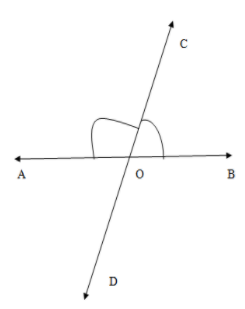
We observe that we have obtained four angles $\angle AOC,\angle BOC,\angle AOD,\angle BOD$ . We know that a straight angle is an angle on a straight line. A straight angle is always measured as ${{180}^{\circ }}$. We have a pair of straight angles above and below the line $AB$ which is $\angle AOB={{180}^{\circ }}$. Similarly we have two straight angles on both left and right side of the straight line $CD$ which is $\angle COD={{180}^{\circ }}$.
We observe angles subtended by ray $\overrightarrow{OC}$ above the line $AB$ whose sum is $\angle AOB$ and angles subtended by the ray $\overrightarrow{OD}$ below the line $AB$ whose sum is also $\angle AOB$. We have
\[\begin{align}
  & \angle AOC+\angle BOC=\angle AOB={{180}^{\circ }} \\
 & \angle AOD+\angle BOD=\angle AOB={{180}^{\circ }} \\
\end{align}\]
So the pair of angles $\angle AOC,\angle BOC$ and the pair of angles $\angle AOD,\angle BOD$ are supplementary angles. We also have angles subtended by ray $\overrightarrow{OA}$ on the left side of the line $CD$ whose sum is $\angle COD$ and angles subtended by the ray $\overrightarrow{OB}$ on the right side of the line $CD$ whose sum is also $\angle COD$. We have

\[\begin{align}
  & \angle AOC+\angle AOD=\angle COD={{180}^{\circ }} \\
 & \angle BOC+\angle BOD=\angle COD={{180}^{\circ }} \\
\end{align}\]
So the pair of angles $\angle AOC,\angle AOD $ and the pair of angles $\angle BOC,\angle BOD$ are supplementary angles. The supplementary angles can also exist not subtended on a straight line. \[\]
 

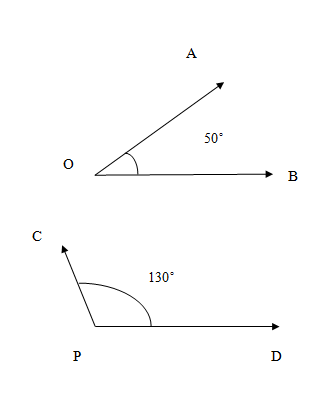
The above angles $\angle AOB,\angle CPD$ are not subtended on straight line but they are supplementary angles because $\angle AOB+\angle CPD={{30}^{\circ }}+{{150}^{\circ }}={{180}^{\circ }}$\[\]

Note: We note that supplementary angles are different from complementary angles which are a pair of angles whose sum of measure is a measurement of a right angle which is ${{90}^{\circ }}$. The sum of two supplementary angles in radian in $\pi .$ Some well known examples of supplementary angles are the adjacent angles of a parallelogram, co-interior angles, the opposite angles of a quadrilateral inscribed in a circle etc.