Question

Define the moment of inertia. State its SI unit and dimensions.

Answer 1

Hint: In this question, we define the Moment of inertia of a body as its ability to remain in the present, the present state is either a state of rest or a state of motion with a constant angular velocity. Then by using the expression for moment of inertia that is \[I = \sum\limits_{i = 1}^n {{M_i}x_i^2} \] we can find SI unit and dimension of the moment of inertia because we already know the dimension of mass M and distance x.

Complete answer:
We know that every physical quantity is either categorized as linear and angular based on their motion, that is it is in linear or rotational motions respectively.
The inertia of a body with linear motion is defined as its ability to remain in the present state that may be a state of rest or moving with the constant velocity. Therefore Greater the inertia of a body the greater is the force required to interrupt its present state. The mass of a body is equal to its linear inertia
Moment of inertia comes into picture when we consider a rotational motion that is the inertia of rotation of a body. In other words, the Moment of inertia is defined as its ability to remain in the present state that may be a state of rest or moving with the constant angular velocity. Therefore Greater the moment of inertia of a body the greater is the torque is required to interrupt its present state.
We can also define the moment of inertia as the sum of the products of the masses of all the particles forming the object and the square of the perpendicular distances of the particles from the axis of rotation of that object as can be seen from the figure 1. That is
\[I = \sum\limits_{i = 1}^n {{M_i}x_i^2} \]
Here \[{M_i}\] is the mass of the \[{i^{th}}\] particle.
 And \[{x_i}\] is the perpendicular distance of the particle from the axis of rotation.

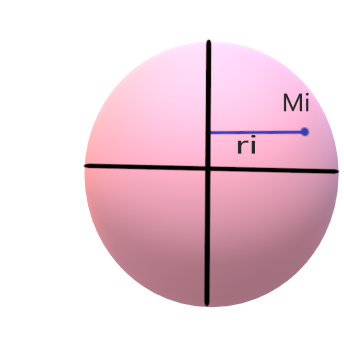
                                                                            Figure 1


As can be seen from the above expression that the SI unit of moment of inertia is $Kg{m^2}$
We can calculate the dimensional formula from the SI unit that is

$ \Rightarrow Kg{m^2} = \left[ {{M^1}{L^0}{T^0}} \right]\left[ {{M^0}{L^2}{T^0}} \right]$
$ \Rightarrow \left[ {{M^1}{L^2}{T^0}} \right]$
So dimensional formula of moment of inertia is $\left[ {{M^1}{L^2}{T^0}} \right]$

Note: for these types of questions we need to have a good understanding of inertia, moment of inertia, forces, torque, linear and rotational motion, and also about their expressions. We need to know how to find the moment of inertia for different types of shapes. We also need to know how to calculate dimensional formulas using SI units and remember dimensional formulas of some basic quantity.