Question

Define the orthocenter of the triangle.

Answer 1

Hint: A triangle is a polygon with three vertices and three edges. The altitude of a triangle is that line that passes through its vertex and is perpendicular to the opposite side. This means that a triangle can have three altitudes, one from each vertex. Vertex means a point where two or more lines meet. The term ortho means right. Hence, the orthocenter indicates the centre of all the right angles from the vertices to the opposite sides i.e., the altitudes.

Complete step-by-step answer:

The orthocenter of a triangle is the point where the perpendicular drawn from the vertices to the opposite sides of the triangle intersect each other. In other words, it is a point where the three altitudes of a triangle meet. An altitude is a line that goes through a vertex (corner point) and is at right angle to the opposite side.
We also know that the orthocenter will vary for different types of triangles such as Isosceles, Equilateral, Scalene, right-angled, etc.
Now, in case of an equilateral triangle, the centroid will be the orthocenter. But in the case of other triangles, the position will be different.
One most important thing is that, orthocenter doesn’t need to lie inside the triangle only. Because in case of an obtuse triangle, it lies outside of the triangle.
The formula of the orthocenter is used to find its coordinates.
i.e. to calculate the slope of the sides of the triangle and perpendicular slope of a line.
Lastly, to construct the orthocenter of a triangle, there is no particular formula but we have to get the coordinates of the vertices of the triangle.
Hence, the orthocenter is the point where all the three altitudes of the triangle cut or intersect each other.
Example of orthocenter:

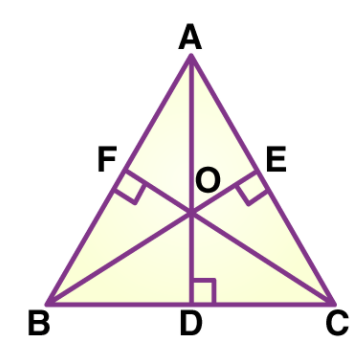
Here “O” is the orthocenter.

Note: Since, the orthocenter is different for all different types of triangle. For an acute angle triangle, the orthocenter lies inside the triangle. Then, for the obtuse angle triangle, the orthocenter lies outside the triangle. And, for a right triangle, the orthocenter lies on the vertex of the right angle. Also, the product of the parts into which the orthocenter divides an altitude is the equivalent for all 3 perpendiculars. Hence, if we are able to find the slopes of the two sides of the triangle then we can find the orthocenter and it’s not necessary to find the slope for the third side also.