Question

What is the definition of exponential decay?

Answer 1

Hint: A quantity is subjected to exponential decay if it decreases at a rate proportional to its current value. Exponential decay is the decrease in a quantity N according to the law $N\left( t \right)={{N}_{0}}{{e}^{-\lambda t}}$ , where $\lambda $ is a positive number called the decay constant of the decaying quantity. We have to derive this formula from $\dfrac{dN}{dt}=-\lambda N$ by rearranging the terms, integrating and taking the exponents.

Complete step-by-step answer:
Let us see the definition of exponential decay. We can say that a quantity is subjected to exponential decay if it decreases at a rate proportional to its current value. The decay law calculates the number of undecayed nuclei in a given radioactive substance.
Let us see the formula for Half-Life in Exponential Decay. Half-life is the length of time it takes an exponentially decaying quantity to decrease to half its original amount. The formula for Half-Life in Exponential Decay is given as
$\Rightarrow\boxed{ N\left( t \right)={{N}_{0}}{{\left( \dfrac{1}{2} \right)}^{\dfrac{t}{{{t}_{1/2}}}}}}$
where ${{N}_{0}}$ is the initial quantity of the substance that will decay (this quantity may be measured in grams, moles, number of atoms, etc.), N(t) is the quantity that still remains and has not yet decayed after a time t and ${{t}_{1/2}}$ is the half-life of the decaying quantity.
We can also write the decay formula as
$\Rightarrow\boxed{ N\left( t \right)={{N}_{0}}{{e}^{\dfrac{-t}{\tau }}}}$
where $\tau $ is a positive number called the mean lifetime of the decaying quantity.
We mainly use the below formula for exponential decay.
Exponential decay is described by the first-order ordinary differential equation.
$\dfrac{dN}{dt}=-\lambda N$
Let us rearrange this equation.
$\dfrac{dN}{N}=-\lambda dt$
Let us integrate both the sides.
$\begin{align}
  & \Rightarrow \int{\dfrac{dN}{N}}=\int{-\lambda dt} \\
 & \Rightarrow \int{\dfrac{dN}{N}}=-\lambda \int{dt} \\
\end{align}$
We know that $\int{\dfrac{dx}{x}}=\ln x$ and $\int{dx}=x$ .
$\Rightarrow \ln N=-\lambda t+C$
Let us take exponents on both the sides.
\[\Rightarrow {{e}^{\ln N}}={{e}^{-\lambda t+C}}\]
We know that ${{e}^{\ln x}}=x$ and ${{a}^{m}}\times {{a}^{n}}={{a}^{m+n}}$ .
\[\Rightarrow N\left( t \right)={{e}^{-\lambda t}}{{e}^{C}}\]
Let us denote ${{e}^{C}}$ as ${{N}_{0}}$ . This s obtained by evaluating the equation at t = 0, as ${{N}_{0}}$ is defined as being the quantity at $t=0$ .
$\Rightarrow \boxed{ N\left( t \right)={{N}_{0}}{{e}^{-\lambda t}}}$
where $\lambda $ is a positive number called the decay constant of the decaying quantity.
We can also relate the parameters ${{t}_{1/2}}$ , $\tau $ and $\lambda $ .
When comparing the above three formulas, we will get
${{\left( \dfrac{1}{2} \right)}^{\dfrac{t}{{{t}_{1/2}}}}}={{e}^{\dfrac{-t}{\tau }}}={{e}^{-\lambda t}}$
Let us take the natural logarithms on both sides.
$\ln {{\left( \dfrac{1}{2} \right)}^{\dfrac{t}{{{t}_{1/2}}}}}=\ln \left( {{e}^{\dfrac{-t}{\tau }}} \right)=\ln \left( {{e}^{-\lambda t}} \right)$
We know that $\ln \left( {{x}^{a}} \right)=a\ln x$ and $\ln {{e}^{x}}=x$ . Hence, the above equation can be written as
$\Rightarrow \dfrac{t}{{{t}_{1/2}}}\ln \left( \dfrac{1}{2} \right)=\dfrac{-t}{\tau }=-\lambda t$
Let us cancel t from all the terms.
$\Rightarrow \dfrac{1}{{{t}_{1/2}}}\ln \left( \dfrac{1}{2} \right)=\dfrac{-1}{\tau }=-\lambda $
Let us consider $\dfrac{1}{{{t}_{1/2}}}\ln \left( \dfrac{1}{2} \right)=\dfrac{-1}{\tau }$ . We have to take ${{t}_{1/2}}$ to the RHS.
$\Rightarrow \ln \left( \dfrac{1}{2} \right)=\dfrac{-{{t}_{1/2}}}{\tau }$
We know that $\ln \left( \dfrac{a}{b} \right)=\ln a-\ln b$ .
$\Rightarrow \ln 1-\ln 2=\dfrac{-{{t}_{1/2}}}{\tau }$
We know that $\ln 1=0$ .
$\Rightarrow -\ln 2=\dfrac{-{{t}_{1/2}}}{\tau }$
Let us cancel the negative sign from both the sides.
$\Rightarrow \ln 2=\dfrac{{{t}_{1/2}}}{\tau }$
Let us take $\tau $ to the LHS.
$\Rightarrow {{t}_{1/2}}=\tau \ln 2...\left( i \right)$
Now, let us consider $\Rightarrow \dfrac{1}{{{t}_{1/2}}}\ln \left( \dfrac{1}{2} \right)=-\lambda $
Similarly, when we solve the LHS, we will get
$\Rightarrow \ln 2=\lambda {{t}_{1/2}}$
Let us take $\lambda $ to the LHS.
$\Rightarrow {{t}_{1/2}}=\dfrac{\ln 2}{\lambda }...\left( ii \right)$
From (i) and (ii), we can write
$\Rightarrow \boxed{ {{t}_{1/2}}=\tau \ln 2=\dfrac{\ln 2}{\lambda }}$
Let us consider ${{t}_{1/2}}=\dfrac{\ln 2}{\lambda }$ .
We know that $\ln 2=0.693$
$\Rightarrow {{t}_{1/2}}=\dfrac{0.693}{\lambda }$
Let us take $\lambda $ to the LHS and t to the RHS.
$\Rightarrow\boxed{ \lambda =\dfrac{0.693}{{{t}_{1/2}}}}$
Decay constant ($\lambda $ ) gives the ratio of number of radioactive atoms decayed to the initial number of atoms.
The graph of exponential decay is shown below for the function $f\left( x \right)={{e}^{-x}}$ .

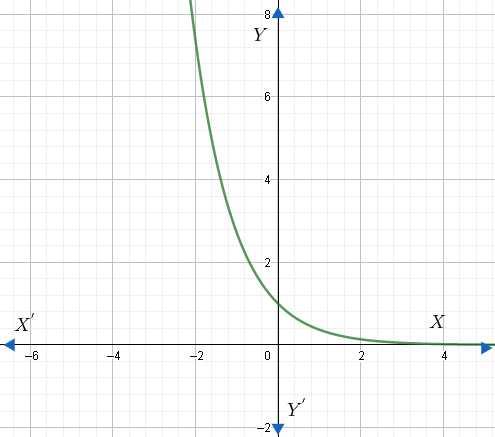
Therefore, exponential decay is the decrease in a quantity N according to the law $N\left( t \right)={{N}_{0}}{{e}^{-\lambda t}}$ .


Note: Students may get confused with exponential growth and exponential decay. xponential growth occurs when the growth rate of the value of a mathematical function is proportional to the function’s current value, resulting in its growth with time being an exponential function. The formula for exponential growth is $P\left( t \right)={{P}_{0}}{{e}^{rt}}$ , where t is the time (number of periods), P(t) is the amount of some quantity at time t, ${{P}_{0}}$ is the initial amount at time $t=0$ , r is the the growth rate and e is the Euler’s number = 2.71828.