Question

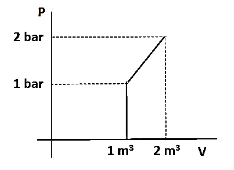
What is the $ \Delta {\text{U}} $ for the process described by the figure. Heat supplied during the process q = 100 KJ.

(A) 50 kJ
(B) $ - 50{\text{ kJ}} $
(C) $ - 150{\text{ kJ}} $
(D) $ + 150{\text{ kJ}} $

Answer 1

Hint: This problem is based on the first law of thermodynamics, which states that, the amount of heat energy supplied to a system is used in two ways: Firstly to increase the internal energy of the system and secondly to perform external pressure-volume work. Mathematically, it can be expressed as:

Formula used: $ \Delta {\text{U = q}} + {\text{w}} $ , Where q represents the change in enthalpy or heat content and $ \Delta {\text{U}} $ , the change in the internal energy of the system.

Complete Stepwise Solution:
Given that, the heat supplied during the process $ q = - 100{\text{ KJ}} $ ( since heat is absorbed by the system).
From the first law of thermodynamics, we know that,
 $ \Delta {\text{U = q}} + {\text{w}} $ ,
The pressure-volume work done can be calculated from the area under the curve = the area of the trapezium = $ \dfrac{1}{2}\left( {{\text{a}} + {\text{b}}} \right){\text{ h}} $
Where, a is the length of the smallest side, b is the length of the largest side and h is the height of the trapezium. Here, a = 1, b = 2 and h = 1, therefore the work done is,
 $ \Delta \left( {{\text{PV}}} \right) $ = $ \dfrac{1}{2}\left( {1 + 2} \right) \times 1 = \dfrac{3}{2} $ .
Hence, the work done = $ \dfrac{3}{2} $ $ {\text{bar/}}{{\text{m}}^{\text{3}}} $ . We need to convert the work in KJ as the heat is expressed in that unit.
Since, 1 $ {\text{bar/}}{{\text{m}}^{\text{3}}} $ = 100 kJ, $ \dfrac{3}{2} $ $ {\text{bar/}}{{\text{m}}^{\text{3}}} $ = 150 kJ.
Therefore, the change in the internal energy is equal to,
 $ \Delta {\text{U }} = - 100 + 150 $ = 50 KJ of energy.
Hence, the correct answer is option A.

Note:
The first law of thermodynamics is based on the universal law of energy that states that the energy of the Universe is constant and it can neither be created nor be destroyed, but it can only be transferred from one form to another.