
What is the derivative graph of a parabola?
Answer
428.7k+ views
Hint: In this problem we need to find the derivative graph of a parabola. For this we will first assume the standard equation of the parabola which is given by
Complete step-by-step answer:
Let the equation of the parabola will be
Differentiating the above equation with respect to
Applying the differentiation for each term individually, then we will have
Taking out the constants from differentiation which are in multiplication with the variables in the above equation, then we will get
From the differentiation formula
We have the value
The value
Simplifying the above equation by using the basic mathematical operations, then we will get
The equation
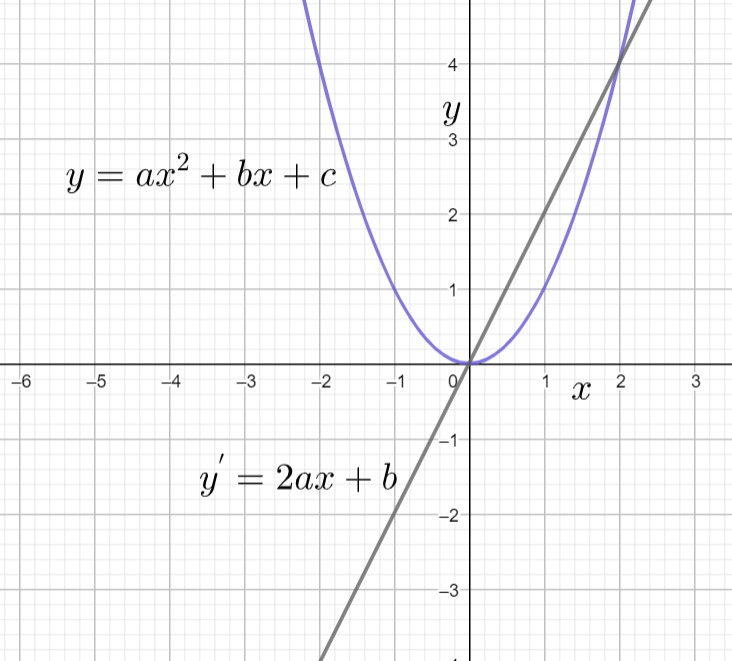
Hence the derivative graph of the parabola is Straight Line.
Note: In this problem we have assumed the equation of the parabola as
Complete step-by-step answer:
Let the equation of the parabola will be
Differentiating the above equation with respect to
Applying the differentiation for each term individually, then we will have
Taking out the constants from differentiation which are in multiplication with the variables in the above equation, then we will get
From the differentiation formula
We have the value
The value
Simplifying the above equation by using the basic mathematical operations, then we will get
The equation

Hence the derivative graph of the parabola is Straight Line.
Note: In this problem we have assumed the equation of the parabola as
Recently Updated Pages
Express the following as a fraction and simplify a class 7 maths CBSE

The length and width of a rectangle are in ratio of class 7 maths CBSE

The ratio of the income to the expenditure of a family class 7 maths CBSE

How do you write 025 million in scientific notatio class 7 maths CBSE

How do you convert 295 meters per second to kilometers class 7 maths CBSE

Write the following in Roman numerals 25819 class 7 maths CBSE

Trending doubts
What are Quantum numbers Explain the quantum number class 11 chemistry CBSE

Write the differences between monocot plants and dicot class 11 biology CBSE

Who built the Grand Trunk Road AChandragupta Maurya class 11 social science CBSE

The reason why India adopted the policy of nonalignment class 11 social science CBSE

How much is 23 kg in pounds class 11 chemistry CBSE

The plastids which are coloured green and colourless class 11 biology CBSE




