
Derive an expression for electric potential at point due to an electric dipole.
Discuss the special cases.
Answer
468.3k+ views
Hint: An electric dipole is a pair of two charges equal in magnitude (q) but opposite in nature (i.e. one is a positive charge and other is a negative charge). The two charges are separated by a distance of length 2a.
Formula used:
Complete step by step answer:
An electric dipole is a pair of two charges equal in magnitude (q) but opposite in nature (i.e. one is a positive charge and other is a negative charge). The two charges are separated by a distance of length 2a.
An electric dipole has a quantity called its dipole moment given by P=2qa.
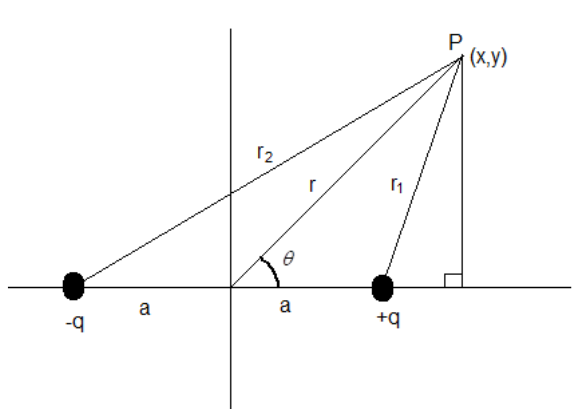
A sketch of an electric dipole is shown below.

Let an electric dipole with charges +q and –q lie on x-axis with the origin as the midpoint of the dipole.
Consider a point P at the coordinates (x,y). The distance of the point from origin be r making an angle
Electric potential due to a charge q at a point, which is at a distance r from the charge is given as
Let the potential due to charge +q be
Let the potential due to charge -q be
Let the total electric potential due to both the charges be V.
Since, electric potential is a scalar quantity,
If you see the given figure,
Since, is right-angled triangle,
Substitute the value of
Therefore,
And
Is also a right-angled triangle. Therefore,
Substitute the value of
Therefore,
This implies that
Consider the expression
Open up the brackets.
But
Therefore, expression (1) can be written as
Since r>>>>a,
From the figure we know,
Therefore,
Take
Here,
Any term
Let us use the same concept in equation (2).
Therefore,
Hence, we get that
Therefore,
Thence we can write equation (iii) as
We know that 2qa=P.
Therefore, the electric potential due to an electric dipole at a given point is equal to
Special cases:
(i) When the given point is on the axial line of the dipole (i.e.
Substitute
Therefore,
We know
Hence,
(ii) When the given point is on the equatorial axis of the dipole (i.e.
Substitute
Therefore,
We know
Hence,
Therefore, when the given point is on the equatorial axis, the electric potential is zero.
Note: You may be thinking about the condition on r that it should be very much greater than a. there is a valid reason for this condition. We study the concept of dipole because molecules exist in the form of dipoles. For example, the bond between oxygen atom and hydrogen atom in water molecules is a dipole moment. You may know that the distance between these atoms is very small and therefore it is negligible when compared to the distance r, from its midpoint.
Formula used:
Complete step by step answer:
An electric dipole is a pair of two charges equal in magnitude (q) but opposite in nature (i.e. one is a positive charge and other is a negative charge). The two charges are separated by a distance of length 2a.
An electric dipole has a quantity called its dipole moment given by P=2qa.
A sketch of an electric dipole is shown below.

Let an electric dipole with charges +q and –q lie on x-axis with the origin as the midpoint of the dipole.
Consider a point P at the coordinates (x,y). The distance of the point from origin be r making an angle

Electric potential due to a charge q at a point, which is at a distance r from the charge is given as
Let the potential due to charge +q be
Let the potential due to charge -q be
Let the total electric potential due to both the charges be V.
Since, electric potential is a scalar quantity,
If you see the given figure,
Since, is right-angled triangle,
Substitute the value of
Therefore,
And
Is also a right-angled triangle. Therefore,
Substitute the value of
Therefore,
This implies that
Consider the expression
Open up the brackets.
But
Therefore, expression (1) can be written as
Since r>>>>a,
From the figure we know,
Therefore,
Take
Here,
Any term
Let us use the same concept in equation (2).
Therefore,
Hence, we get that
Therefore,
Thence we can write equation (iii) as
We know that 2qa=P.
Therefore, the electric potential due to an electric dipole at a given point is equal to
Special cases:
(i) When the given point is on the axial line of the dipole (i.e.
Substitute
Therefore,
We know
Hence,
(ii) When the given point is on the equatorial axis of the dipole (i.e.
Substitute
Therefore,
We know
Hence,
Therefore, when the given point is on the equatorial axis, the electric potential is zero.
Note: You may be thinking about the condition on r that it should be very much greater than a. there is a valid reason for this condition. We study the concept of dipole because molecules exist in the form of dipoles. For example, the bond between oxygen atom and hydrogen atom in water molecules is a dipole moment. You may know that the distance between these atoms is very small and therefore it is negligible when compared to the distance r, from its midpoint.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Class 12 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Economics: Engaging Questions & Answers for Success

Trending doubts
Draw a labelled sketch of the human eye class 12 physics CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Which one of the following is a true fish A Jellyfish class 12 biology CBSE

Why is the cell called the structural and functional class 12 biology CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Write the difference between solid liquid and gas class 12 chemistry CBSE




