
Derive an expression of the magnetic field at the center of a circular current carrying coil.
Answer
427.6k+ views
Hint: A wire carrying current has a magnetic field. The intensity of the magnetic field at any point is obtained by the Biot-Savart’s law.
This law in vector form can be written as
Step by step solution:
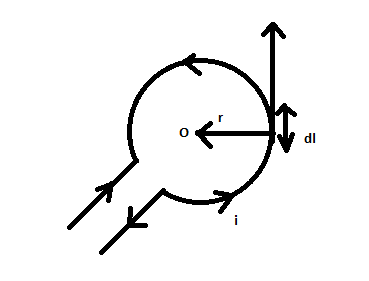
1) Consider a current carrying circular loop having its center at O carrying current i. If dl is a small element at a distance r then, the magnetic field intensity on that point can be written using Biot-Savart’s law.
2) As the loop is circular then,
3) Putting this in the Biot-Savart’s law we will get,
4) If we think that the circular loop is composed of numbers of such small element dl, then we will get the magnetic intensity for all over the loop. So to get the total field we must sum up that is integrate the magnetic field all over the field.
5) As the integration over dl returns the circumference of the loop then, you can write,
Hence the magnetic field at the center of the circular coil is
Note: Field due to a semi-circular coil is just half that of the circular coil.
This law in vector form can be written as
Step by step solution:

1) Consider a current carrying circular loop having its center at O carrying current i. If dl is a small element at a distance r then, the magnetic field intensity on that point can be written using Biot-Savart’s law.
2) As the loop is circular then,
3) Putting this in the Biot-Savart’s law we will get,
4) If we think that the circular loop is composed of numbers of such small element dl, then we will get the magnetic intensity for all over the loop. So to get the total field we must sum up that is integrate the magnetic field all over the field.
5) As the integration over dl returns the circumference of the loop then, you can write,
Hence the magnetic field at the center of the circular coil is
Note: Field due to a semi-circular coil is just half that of the circular coil.
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Give 10 examples of unisexual and bisexual flowers

Draw a labelled sketch of the human eye class 12 physics CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

What are the major means of transport Explain each class 12 social science CBSE

Why is the cell called the structural and functional class 12 biology CBSE




