Question

Derive first equation of motion by graphical method.

Answer 1

Hint: Draw the velocity-time graph of a particle moving from a point A with initial velocity u to a final point B at which the final velocity is v. Make the constructions in the velocity-time graph and determine the final velocity of the particle in terms of initial velocity and acceleration of the particle to derive the expression for first kinematic equation of motion of the particle.

Complete answer:
Suppose a particle of mass \[m\] is moving in a straight line with a uniform acceleration \[a\]. Let the initial velocity \[u\] of the particle changes to final velocity \[v\] when the particle reaches its destination.

We can derive the first law of kinematics for the motion of the particle by graphical method as follows: Let us draw the velocity-time graph of the particle with velocity on Y-axis and time on X-axis.

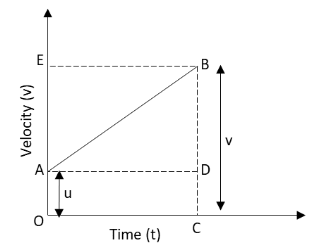
In the above graph, it can be seen that the particle moves from point A to point B. The perpendicular is drawn from point B on the time axis. The line joining point A and perpendicular is drawn.

The initial velocity of the particle in the above graph is given by \[{\text{OA}} = u\].
The final velocity of the particle in the above graph is given by \[{\text{BC}} = v\].
The lengths OA and DC in the above graph are equal.
\[{\text{OA}} = {\text{DC}}\]

From the above graph, we can also write
\[{\text{BC}} = {\text{BD}} + {\text{DC}}\]
Substitute \[{\text{OA}}\] for \[{\text{DC}}\] in the above equation.
\[{\text{BC}} = {\text{BD}} + {\text{OA}}\]

Substitute \[v\] for \[{\text{BC}}\] and \[u\] for \[{\text{OA}}\] in the above equation.
\[v = {\text{BD}} + u\] …… (1)

We know that the slope of the velocity-time graph of a particle is acceleration of the particle.
Hence, the slope of line AB will give the acceleration \[a\] of the particle.
\[a = {\text{slope of AB}}\]

The slope of line AB is given by
\[{\text{slope of AB}} = \dfrac{{{\text{BD}}}}{{{\text{AD}}}}\]
Substitute \[\dfrac{{{\text{BD}}}}{{{\text{AD}}}}\] for \[{\text{slope of AB}}\] in the above equation for acceleration.
\[a = \dfrac{{{\text{BD}}}}{{{\text{AD}}}}\]
Rearrange the above equation for BD.
\[ \Rightarrow {\text{BD}} = a{\text{AD}}\]

From the graph, we can write
\[{\text{AD}} = {\text{OC}} = t\]
Substitute \[t\] for \[{\text{AD}}\] in the above equation for BD.
\[ \Rightarrow {\text{BD}} = at\]
Substitute \[at\] for \[{\text{BD}}\] in equation (1).
\[v = at + u\]
\[ \therefore v = u + at\]
This is the required expression for the first kinematic equation of motion.

Hence, the first kinematic equation of motion is \[v = u + at\].

Note:The students should be careful while taking and equating different distances on the velocity-time graph of the particle. If these distances are not taken correctly, we will not end up with the correct expression for the first kinematic equation of motion of the particle.