
Derive lens maker formula for a convex lens.
Answer
437.1k+ views
2 likes
Hint: For making a lens of desired focal length, the lens maker formula is used. It has to be specified, the refractive index of the lens material, refractive index of the surroundings, and the radii of curvatures of two spheres of which the lens is a part of. We will use the expression for the refraction of lightwave on a spherical surface to find the required lens maker formula.
Formula used:
Refraction at first surface,
Refraction at second surface,
Complete step by step answer:
Lenses having different values of focal lengths are used for making various optical instruments. The focal length of an optical lens depends upon the refractive index of the material which was used to make the lens and the radii of curvatures of the two surfaces, of which the lens is a part of.
Assumptions for lens maker formula,
Let us consider a thin lens with two refracting surfaces having radii of curvatures
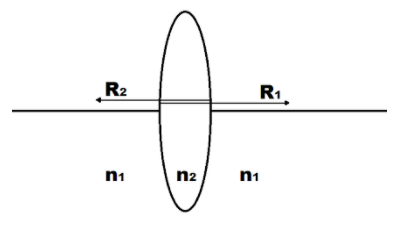
With the help of formula for refraction at a single spherical surface,
For the first surface, we have,
For the second surface, we have,
Adding the above two equations,
When
We get,
Therefore,
Where,
The above equation is known as the Lens maker formula.
Lens manufacturers commonly take the help of the lens maker formula for manufacturing the lenses of the desired focal length.
Additional information:
In optics, the relation between the distance of an image
Expression for Lens maker formula:
Derivation for lens maker formula:
Consider a convex lens having an optical centre at
A real, inverted, and magnified image
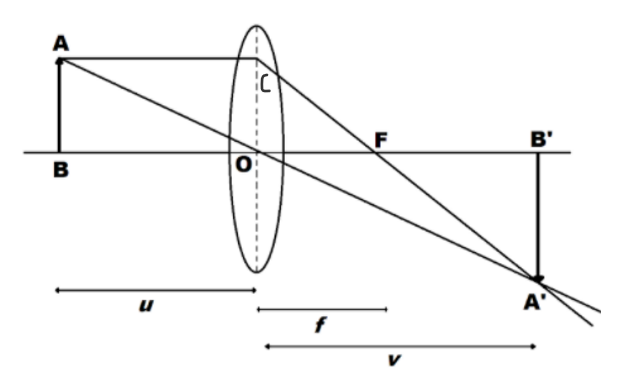
From the above figure,
Therefore,
Similarly,
Therefore,
Also,
Thus,
Equating the above equations, we get,
Therefore,
Substituting the sign convention, we get,
Diving both the sides by
The above equation is known as Lens formula.
Note: While deriving the lens formula, it should be remembered that the image distance from the refraction at the first surface becomes the object distance for the refraction at the second surface since the light ray is passing undisturbed from the lens. Also, the refractive indices of the two spherical materials, of which the lens is a part of, can also be different. In the above derivation, we have taken the refractive indices of both the material as the same.
Formula used:
Refraction at first surface,
Refraction at second surface,
Complete step by step answer:
Lenses having different values of focal lengths are used for making various optical instruments. The focal length of an optical lens depends upon the refractive index of the material which was used to make the lens and the radii of curvatures of the two surfaces, of which the lens is a part of.
Assumptions for lens maker formula,
Let us consider a thin lens with two refracting surfaces having radii of curvatures

With the help of formula for refraction at a single spherical surface,
For the first surface, we have,
For the second surface, we have,
Adding the above two equations,
When
We get,
Therefore,
Where,
The above equation is known as the Lens maker formula.
Lens manufacturers commonly take the help of the lens maker formula for manufacturing the lenses of the desired focal length.
Additional information:
In optics, the relation between the distance of an image
Expression for Lens maker formula:
Derivation for lens maker formula:
Consider a convex lens having an optical centre at
A real, inverted, and magnified image

From the above figure,
Therefore,
Similarly,
Therefore,
Also,
Thus,
Equating the above equations, we get,
Therefore,
Substituting the sign convention, we get,
Diving both the sides by
The above equation is known as Lens formula.
Note: While deriving the lens formula, it should be remembered that the image distance from the refraction at the first surface becomes the object distance for the refraction at the second surface since the light ray is passing undisturbed from the lens. Also, the refractive indices of the two spherical materials, of which the lens is a part of, can also be different. In the above derivation, we have taken the refractive indices of both the material as the same.
Recently Updated Pages
Master Class 4 Maths: Engaging Questions & Answers for Success

Master Class 4 English: Engaging Questions & Answers for Success

Master Class 4 Science: Engaging Questions & Answers for Success

Class 4 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Trending doubts
Give 10 examples of unisexual and bisexual flowers

Draw a labelled sketch of the human eye class 12 physics CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

What are the major means of transport Explain each class 12 social science CBSE

What is the difference between resemblance and sem class 12 social science CBSE




