
Derive Lens Maker’s formula for a convex lens.
Answer
568.8k+ views
Hint: A convex lens or a biconvex lens has two convex surfaces. We use the formula for refraction through convex surfaces to both these convex surfaces and add them, to derive the Lens Maker’s formula. Refraction through a convex surface is dependent on the nature of the medium as well as the radius of curvature of the surface, through which refraction takes place.
Complete step by step answer:
Let us consider a convex lens as shown in the figure. It consists of two convex surfaces $XPY$ and $XQY$ of radii ${{R}_{1}}$ and ${{R}_{2}}$, respectively. Let the refractive index of the medium inside the lens be ${{\mu }_{2}}$ and the refractive index of the medium outside the lens be ${{\mu }_{1}}$.
Usually, when we use a lens, the medium inside the lens turns out to be denser than the surrounding medium. Therefore, let us consider ${{\mu }_{2}}$ to be a denser medium and ${{\mu }_{1}}$ to be a rarer medium.
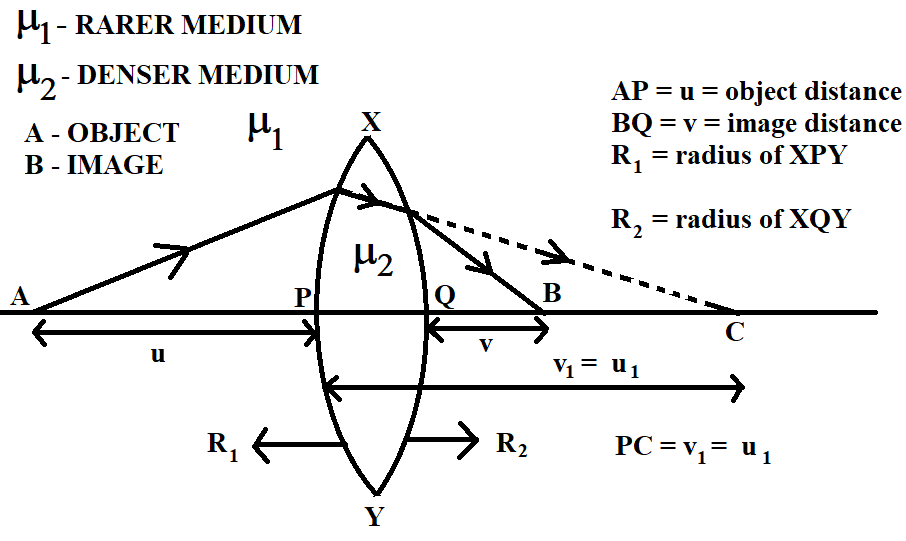
Firstly, let us consider refraction through the convex surface $XPY$. An object is placed on the left side of the lens (at A). Let the distance of this object from the centre of the convex surface $XPY$ be $u$. Light rays from the object passes from rarer medium ${{\mu }_{1}}$ to denser medium ${{\mu }_{2}}$. Light rays get refracted through $XPY$ and an image of the object is formed on the other side of the surface (at C), as shown in the figure. Let us call the image distance, from the centre of $XPY$, ${{v}_{1}}$. We know that refraction through a convex surface from a rarer medium to a denser medium is given by
$\dfrac{{{\mu }_{1}}}{u}+\dfrac{{{\mu }_{2}}}{v}=\dfrac{\left( {{\mu }_{2}}-{{\mu }_{1}} \right)}{R}$
where
${{\mu }_{1}}$ is the refractive index of rarer medium
${{\mu }_{2}}$ is the refractive index of denser medium
$u$ is the object distance
$v$ is the image distance
$R$ is the radius of convex surface
Let this be equation 1.
Applying equation 1 to the case of refraction through $XPY$, we have
$\dfrac{{{\mu }_{1}}}{-u}+\dfrac{{{\mu }_{2}}}{{{v}_{1}}}=\dfrac{\left( {{\mu }_{2}}-{{\mu }_{1}} \right)}{{{R}_{1}}}$
where
${{\mu }_{1}}$ is the refractive index of rarer medium, to the left of $XPY$
${{\mu }_{2}}$ is the refractive index of denser medium, to the right of $XPY$
$u$ is the object distance
${{v}_{1}}$ is the image distance
${{R}_{1}}$ is the radius of convex surface $XPY$
Let this be equation 2.
Now, let us move on to the refraction happening through the other convex surface of the lens, $XQY$. Here, the object is assumed to be the image obtained (at C), after the first refraction through $XPY$. Therefore, object distance in this case is equal to the image distance, we obtained after refraction through $XPY$. Let us call this object distance ${{u}_{1}}$. Clearly,
${{u}_{1}}={{v}_{1}}$
We also assume that the refraction happening here is from denser medium to rarer medium, as if the object is placed in denser medium. After refraction $XQY$, the final image is formed at B, as shown in the figure. We know that refraction through a convex surface from a denser medium to a rarer medium is given by
$\dfrac{{{\mu }_{2}}}{u}+\dfrac{{{\mu }_{1}}}{v}=\dfrac{\left( {{\mu }_{1}}-{{\mu }_{2}} \right)}{R}$
where
${{\mu }_{1}}$ is the refractive index of rarer medium
${{\mu }_{2}}$ is the refractive index of denser medium
$u$ is the object distance
$v$ is the image distance
$R$ is the radius of convex surface
Let this be equation 3.
Applying equation 3 to the case of refraction through $XQY$, we have
$\dfrac{{{\mu }_{2}}}{-{{u}_{1}}}+\dfrac{{{\mu }_{1}}}{v}=\dfrac{\left( {{\mu }_{1}}-{{\mu }_{2}} \right)}{{{R}_{2}}}$
where
${{\mu }_{1}}$ is the refractive index of rarer medium, to the right of $XQY$
${{\mu }_{2}}$ is the refractive index of denser medium, to the left of $XQY$
${{u}_{1}}$ is the object distance
$v$ is the image distance
${{R}_{2}}$ is the radius of convex surface $XQY$
Let this be equation 4.
Now, to get the combined refraction through both the convex surfaces, as if the case of refraction through a convex lens, let us add equation 2 and equation 4. We have
$\dfrac{{{\mu }_{1}}}{-u}+\dfrac{{{\mu }_{2}}}{{{v}_{1}}}+\dfrac{{{\mu }_{2}}}{-{{u}_{1}}}+\dfrac{{{\mu }_{1}}}{v}=\dfrac{\left( {{\mu }_{2}}-{{\mu }_{1}} \right)}{{{R}_{1}}}+\dfrac{\left( {{\mu }_{1}}-{{\mu }_{2}} \right)}{{{R}_{2}}}$
Let this be equation 5.
Here, we know that
${{v}_{1}}={{u}_{1}}$
Therefore, equation 5 becomes
$\dfrac{{{\mu }_{1}}}{-u}+\dfrac{{{\mu }_{1}}}{v}=\dfrac{\left( {{\mu }_{2}}-{{\mu }_{1}} \right)}{{{R}_{1}}}+\dfrac{\left( {{\mu }_{1}}-{{\mu }_{2}} \right)}{{{R}_{2}}}$
Taking $({{\mu }_{2}}-{{\mu }_{1}})$ outside, we have
\[\dfrac{{{\mu }_{1}}}{-u}+\dfrac{{{\mu }_{1}}}{v}=\left( {{\mu }_{2}}-{{\mu }_{1}} \right)\left( \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right)\Rightarrow \dfrac{1}{v}-\dfrac{1}{u}=\dfrac{\left( {{\mu }_{2}}-{{\mu }_{1}} \right)}{{{\mu }_{1}}}\left( \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right)\Rightarrow \dfrac{1}{v}-\dfrac{1}{u}=\left( \dfrac{{{\mu }_{2}}}{{{\mu }_{1}}}-1 \right)\left( \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right)\]
We know that
$\dfrac{{{\mu }_{2}}}{{{\mu }_{1}}}={{\mu }_{21}}$
where
${{\mu }_{21}}$ is the refractive index of convex lens with respect to the surrounding medium
We also know that
$\dfrac{1}{v}-\dfrac{1}{u}=\dfrac{1}{f}$
where
$f$ is the focal length of convex lens
Substituting these values in the above expression, we have
\[\dfrac{1}{v}-\dfrac{1}{u}=\left( \dfrac{{{\mu }_{2}}}{{{\mu }_{1}}}-1 \right)\left( \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right)\Rightarrow \dfrac{1}{f}=\left( {{\mu }_{21}}-1 \right)\left( \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right)\]
Let this be equation 6.
Equation 6 is nothing but Lens Maker’s formula. Explaining the terms in Lens Maker’s formula, we have
\[\dfrac{1}{f}=\left( {{\mu }_{21}}-1 \right)\left( \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right)\]
where
$f$ is the focal length of convex lens
${{\mu }_{21}}$ is the refractive index of convex lens with respect to the surrounding medium
${{R}_{1}}$ is the radius of curvature of convex lens, close to the object
${{R}_{2}}$ is the radius of curvature of convex lens, away from the object
Hence, the derivation.
Note:
Refraction through convex surfaces follows sign convention. For convenience, parameters on the left side of the surface are taken as negative and the parameters on the right side of the surface are taken as positive. Clearly, object distances in the first case as well as the second case are taken as negative and the corresponding image distances turn out to be positive. Since the radius of curvature falls on the right side in each case of refraction, it is taken to be positive always. This sign convention is followed throughout this writeup and can be clearly seen in equation 2 as well as equation 3.
Complete step by step answer:
Let us consider a convex lens as shown in the figure. It consists of two convex surfaces $XPY$ and $XQY$ of radii ${{R}_{1}}$ and ${{R}_{2}}$, respectively. Let the refractive index of the medium inside the lens be ${{\mu }_{2}}$ and the refractive index of the medium outside the lens be ${{\mu }_{1}}$.
Usually, when we use a lens, the medium inside the lens turns out to be denser than the surrounding medium. Therefore, let us consider ${{\mu }_{2}}$ to be a denser medium and ${{\mu }_{1}}$ to be a rarer medium.

Firstly, let us consider refraction through the convex surface $XPY$. An object is placed on the left side of the lens (at A). Let the distance of this object from the centre of the convex surface $XPY$ be $u$. Light rays from the object passes from rarer medium ${{\mu }_{1}}$ to denser medium ${{\mu }_{2}}$. Light rays get refracted through $XPY$ and an image of the object is formed on the other side of the surface (at C), as shown in the figure. Let us call the image distance, from the centre of $XPY$, ${{v}_{1}}$. We know that refraction through a convex surface from a rarer medium to a denser medium is given by
$\dfrac{{{\mu }_{1}}}{u}+\dfrac{{{\mu }_{2}}}{v}=\dfrac{\left( {{\mu }_{2}}-{{\mu }_{1}} \right)}{R}$
where
${{\mu }_{1}}$ is the refractive index of rarer medium
${{\mu }_{2}}$ is the refractive index of denser medium
$u$ is the object distance
$v$ is the image distance
$R$ is the radius of convex surface
Let this be equation 1.
Applying equation 1 to the case of refraction through $XPY$, we have
$\dfrac{{{\mu }_{1}}}{-u}+\dfrac{{{\mu }_{2}}}{{{v}_{1}}}=\dfrac{\left( {{\mu }_{2}}-{{\mu }_{1}} \right)}{{{R}_{1}}}$
where
${{\mu }_{1}}$ is the refractive index of rarer medium, to the left of $XPY$
${{\mu }_{2}}$ is the refractive index of denser medium, to the right of $XPY$
$u$ is the object distance
${{v}_{1}}$ is the image distance
${{R}_{1}}$ is the radius of convex surface $XPY$
Let this be equation 2.
Now, let us move on to the refraction happening through the other convex surface of the lens, $XQY$. Here, the object is assumed to be the image obtained (at C), after the first refraction through $XPY$. Therefore, object distance in this case is equal to the image distance, we obtained after refraction through $XPY$. Let us call this object distance ${{u}_{1}}$. Clearly,
${{u}_{1}}={{v}_{1}}$
We also assume that the refraction happening here is from denser medium to rarer medium, as if the object is placed in denser medium. After refraction $XQY$, the final image is formed at B, as shown in the figure. We know that refraction through a convex surface from a denser medium to a rarer medium is given by
$\dfrac{{{\mu }_{2}}}{u}+\dfrac{{{\mu }_{1}}}{v}=\dfrac{\left( {{\mu }_{1}}-{{\mu }_{2}} \right)}{R}$
where
${{\mu }_{1}}$ is the refractive index of rarer medium
${{\mu }_{2}}$ is the refractive index of denser medium
$u$ is the object distance
$v$ is the image distance
$R$ is the radius of convex surface
Let this be equation 3.
Applying equation 3 to the case of refraction through $XQY$, we have
$\dfrac{{{\mu }_{2}}}{-{{u}_{1}}}+\dfrac{{{\mu }_{1}}}{v}=\dfrac{\left( {{\mu }_{1}}-{{\mu }_{2}} \right)}{{{R}_{2}}}$
where
${{\mu }_{1}}$ is the refractive index of rarer medium, to the right of $XQY$
${{\mu }_{2}}$ is the refractive index of denser medium, to the left of $XQY$
${{u}_{1}}$ is the object distance
$v$ is the image distance
${{R}_{2}}$ is the radius of convex surface $XQY$
Let this be equation 4.
Now, to get the combined refraction through both the convex surfaces, as if the case of refraction through a convex lens, let us add equation 2 and equation 4. We have
$\dfrac{{{\mu }_{1}}}{-u}+\dfrac{{{\mu }_{2}}}{{{v}_{1}}}+\dfrac{{{\mu }_{2}}}{-{{u}_{1}}}+\dfrac{{{\mu }_{1}}}{v}=\dfrac{\left( {{\mu }_{2}}-{{\mu }_{1}} \right)}{{{R}_{1}}}+\dfrac{\left( {{\mu }_{1}}-{{\mu }_{2}} \right)}{{{R}_{2}}}$
Let this be equation 5.
Here, we know that
${{v}_{1}}={{u}_{1}}$
Therefore, equation 5 becomes
$\dfrac{{{\mu }_{1}}}{-u}+\dfrac{{{\mu }_{1}}}{v}=\dfrac{\left( {{\mu }_{2}}-{{\mu }_{1}} \right)}{{{R}_{1}}}+\dfrac{\left( {{\mu }_{1}}-{{\mu }_{2}} \right)}{{{R}_{2}}}$
Taking $({{\mu }_{2}}-{{\mu }_{1}})$ outside, we have
\[\dfrac{{{\mu }_{1}}}{-u}+\dfrac{{{\mu }_{1}}}{v}=\left( {{\mu }_{2}}-{{\mu }_{1}} \right)\left( \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right)\Rightarrow \dfrac{1}{v}-\dfrac{1}{u}=\dfrac{\left( {{\mu }_{2}}-{{\mu }_{1}} \right)}{{{\mu }_{1}}}\left( \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right)\Rightarrow \dfrac{1}{v}-\dfrac{1}{u}=\left( \dfrac{{{\mu }_{2}}}{{{\mu }_{1}}}-1 \right)\left( \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right)\]
We know that
$\dfrac{{{\mu }_{2}}}{{{\mu }_{1}}}={{\mu }_{21}}$
where
${{\mu }_{21}}$ is the refractive index of convex lens with respect to the surrounding medium
We also know that
$\dfrac{1}{v}-\dfrac{1}{u}=\dfrac{1}{f}$
where
$f$ is the focal length of convex lens
Substituting these values in the above expression, we have
\[\dfrac{1}{v}-\dfrac{1}{u}=\left( \dfrac{{{\mu }_{2}}}{{{\mu }_{1}}}-1 \right)\left( \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right)\Rightarrow \dfrac{1}{f}=\left( {{\mu }_{21}}-1 \right)\left( \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right)\]
Let this be equation 6.
Equation 6 is nothing but Lens Maker’s formula. Explaining the terms in Lens Maker’s formula, we have
\[\dfrac{1}{f}=\left( {{\mu }_{21}}-1 \right)\left( \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right)\]
where
$f$ is the focal length of convex lens
${{\mu }_{21}}$ is the refractive index of convex lens with respect to the surrounding medium
${{R}_{1}}$ is the radius of curvature of convex lens, close to the object
${{R}_{2}}$ is the radius of curvature of convex lens, away from the object
Hence, the derivation.
Note:
Refraction through convex surfaces follows sign convention. For convenience, parameters on the left side of the surface are taken as negative and the parameters on the right side of the surface are taken as positive. Clearly, object distances in the first case as well as the second case are taken as negative and the corresponding image distances turn out to be positive. Since the radius of curvature falls on the right side in each case of refraction, it is taken to be positive always. This sign convention is followed throughout this writeup and can be clearly seen in equation 2 as well as equation 3.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Trending doubts
What are the major means of transport Explain each class 12 social science CBSE

Which are the Top 10 Largest Countries of the World?

Draw a labelled sketch of the human eye class 12 physics CBSE

How much time does it take to bleed after eating p class 12 biology CBSE

Explain sex determination in humans with line diag class 12 biology CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE




