Question

Derive the balancing condition of a Wheatstone bridge

Answer 1

Hint: First draw the circuit diagram of the Wheatstone’s bridge and then try to analyse the condition. Try to understand the concept of the bridge and obtain the required balanced condition by using the concept of current flow and voltage division.

Complete step by step answer: the Wheatstone’s bridge works on the principle that where the ratio of the resistances are equal no current flows through the galvanometer. In normal condition the galvanometer is in unbalanced condition that is current flows through the galvanometer. When no current flows through the galvanometer it is known as the balanced condition of the galvanometer.

The Wheatstone’s bridge will be in the balanced condition when the current through the galvanometer is zero.

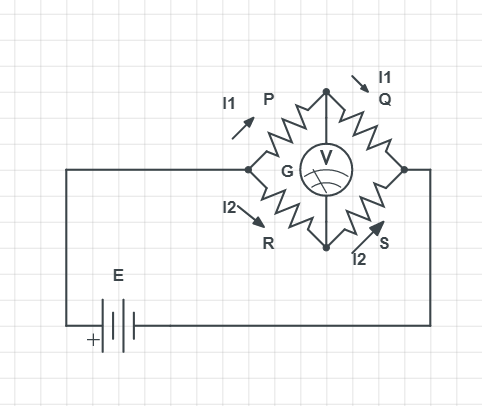
Current will divide in magnitude to ${{I}_{1}}\And {{I}_{2}}$ to go through resistors P and R.
So, ${{I}_{1}}P={{I}_{2}}R$

When no current flows through galvanometer current ${{I}_{1}}$ will go through P and Q and current ${{I}_{2}}$ will go through R and S.

So, we can write.

${{I}_{1}}=\dfrac{E}{P+Q}$ and ${{I}_{2}}=\dfrac{E}{R+S}$

By substituting these values in the above equation, we get that

$\begin{align}
  & \dfrac{E}{P+Q}P=\dfrac{E}{R+S}R \\
 & \dfrac{P}{P+Q}=\dfrac{R}{R+S} \\
 & P\left( R+S \right)=R\left( P+Q \right) \\
 & PR+PS=PR+PQ \\
 & PS=PQ \\
\end{align}$

This is the required condition for a balanced galvanometer.
We can also write it as,

$\dfrac{P}{R}=\dfrac{Q}{S}$

i.e. if the ratio of the resistance connected in the circuit in this way is equal then the galvanometer will be in its balanced condition.

Note: In a wheatstone bridge we have two known resistances and two unknown resistances. From these if we put one resistance with some value then we can find out what value of resistance we should put so that the bridge will be in a balanced condition.