Question

Derive the equation of projectile motion.

Answer 1

Hint: In this question consider an object performing projectile motion and whose velocity is tangential to the path which it is taken. Take the two components of the velocity considering that object’s velocity is making an angle $\theta $ with the origin. Use the equation of motion along with basic distance speed and time relations to get the equation for total time of flight, maximum height that can be reached by the particle and the maximum horizontal distance travelled by the particle.

Complete Step-by-Step solution:

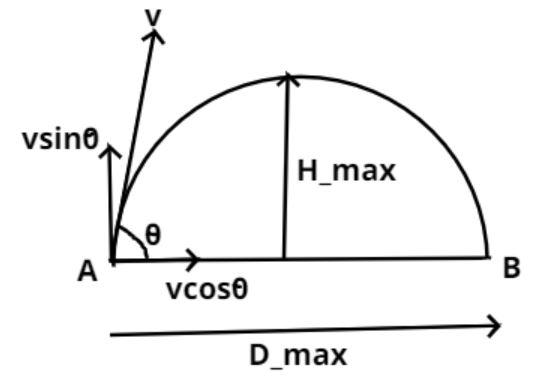
Let an object be thrown with a velocity (v) from point A with an angle $\left( \theta \right)$ with the horizontal x-axis.
So the velocity component along x-axis is given as = ${v_x} = v\cos \theta $,
And the velocity component along the y-axis is given as = ${v_y} = v\sin \theta $.
Now at time (T = 0) there is no displacement along the x and y-axis.
So initial distances are zero along the x and y-axis.
Now at time T = t, displacement $\left( {{S_1}} \right)$ along x-axis is
$ \Rightarrow {S_1} = {v_x}t = v\cos \theta \times t$.................... (1), (as distance is equal to speed multiplied by time).
And the displacement $\left( {{S_2}} \right)$ along y-axis is
$S = ut + \dfrac{1}{2}a{t^2}$ (by second law of motion).
As the object is above the horizontal axis therefore acceleration works on the object downwards therefore a = - g = 9.8 m/$s^2$.
\[ \Rightarrow {S_2} = {v_y}t = v\sin \theta \times t - \dfrac{1}{2}g{t^2}\]..................... (2).
Now as we know that when the particle reaches its maximum height the velocity component of the y-axis should be zero.
$ \Rightarrow {v_y} = 0$
Let the time required to reach the maximum height is ${t_{\max }}$
So from equation (2) substitute the values we have,
\[ \Rightarrow \left( 0 \right)t = v\sin \theta \times t - \dfrac{1}{2}g{t^2}\]
\[ \Rightarrow 0 = v\sin \theta - \dfrac{1}{2}g{t_{\max }}\]
$ \Rightarrow {t_{\max }} = \dfrac{{2v\sin \theta }}{g}$
So this is the maximum time required to reach at the maximum height.
$\left( 1 \right)$ Total time of flight:
Now the total time of the projectile is twice of this time.
So total time of projectile or total time of flight to reach the ground is
= ${T_{\max }} = 2{t_{\max }} = \dfrac{{2v\sin \theta }}{g}$................ (3)
$\left( 2 \right)$ Maximum height reach by the particle:
Let the maximum height be ${H_{\max }}$
Now from third law of motion we have,
${v^2} = {u^2} + 2as$, where u = initial velocity, v = final velocity, a = acceleration, s = distance covered.
As final velocity becomes zero when particle reaches the maximum height and initial velocity is $v\sin \theta $ acceleration is acting downwards so a = -g, and t is time (${t_{\max }}$) to reach the maximum height.
Now substitute the values we have,
\[ \Rightarrow 0 = {\left( {v\sin \theta } \right)^2} - 2g{H_{\max }}\]
Now simplify it we have,
$ \Rightarrow {H_{\max }} = \dfrac{{{{\left( {v\sin \theta } \right)}^2}}}{{2g}}$................ (4)
So this is the maximum height reached by the particle.
$\left( 3 \right)$ Maximum horizontal distance covered by the particle
Let the maximum horizontal distance be ${D_{\max }}$
Now from equation (1) we have,
$ \Rightarrow {S_1} = v\cos \theta \times t$
In this equation ${S_1} = {D_{\max }}$ and t is the total time taken by the particle to reach the ground which is ${T_{\max }}$, now substitute the values we have,
$ \Rightarrow {D_{\max }} = v\cos \theta \times {T_{\max }}$
$ \Rightarrow {D_{\max }} = v\cos \theta \times \dfrac{{2v\sin \theta }}{g} = \dfrac{{{v^2}\sin 2\theta }}{g}$................. (5), $\left[ {\because \sin 2\theta = 2\sin \theta \cos \theta } \right]$
So equations (3), (4) and (5) are the required equations of projectile motion.
So this is the required answer.

Note – A projectile is any object that once projected continues the motion under the influence of gravity without the interference of any external force. By definition only a projectile has only one force: the force of gravity. If an external force starts acting upon the object in between the projectile then it can’t continue the projectile as the path gets changed.