Question

Derive the expression for motional EMF induced in a conductor moving in a uniform magnetic field.

Answer 1

Hint: The magnetic flux enclosed in area A is given by
\[\Phi = BA\]
If the length of the conductor is l and displacement be x then the area A is given by
\[A = lx\]
Hence,
\[\Phi = Blx\]

Complete step by step solution:
1) Consider a straight conducting wire placed in an uniform magnetic field. The length of the wire is AB= l.

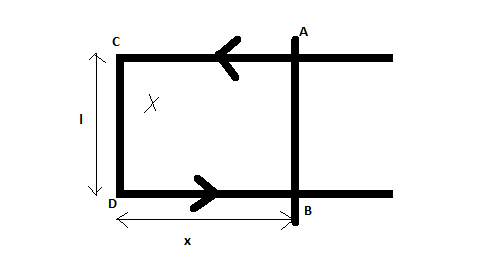
2) Now it is shifted x distance to another point CD.

3) Hence the flux associated with the loop ABCD is given by
\[{\Phi _B} = Blx\]

4) As the displacement x changes with time, then there is a rate of change of induced flux. According to Faraday’s law, this rate of change of flux will induce an emf in the conductor. The rate of change of flux is hence given by
\[
  \varepsilon = - \dfrac{{d{\Phi _B}}}{{dt}} \\
  \varepsilon = - \dfrac{d}{{dt}}(Blx) \\
  \varepsilon = - Bl\dfrac{d}{{dt}}x \\
  \varepsilon = - Blv \\
\]
This induced emf is called the motional emf.

Note: The negative sign given here indicates that this emf opposes the cause of its generation. Faraday’s law of electromagnetic induction gives the concept of motional emf which is different from the emf of the cell and opposes it.