Question

Derive the formula for the force acting between two parallel current carrying conductors.

Answer 1

Hint: Before we proceed to derive the expression for force acting between two current carrying parallel conductors, we should be familiar with the expression for the Biot-Savart’s law which gives the expression for magnetic field at a point due to a current carrying conductor, as follows –
$dB = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{I \cdot dl}}{{{r^3}}}$
where I = current in the circuit, $dl$= length of the current element, r = distance of the point from the current element.

Complete step by step solution:
Consider two conductors A and B of infinite length, with currents ${I_A}$ and ${I_B}$ in the same direction and separated at a distance of d, as shown:

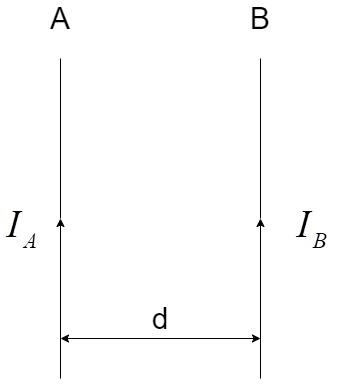
The current ${I_A}$ results in a magnetic field ${B_A}$ at the conductor B, at the distance of d, which is given by applying the Biot-Savart’s law for a conductor carrying current.
${B_A} = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2{I_A}}}{d}$
Whenever a current carrying conductor is placed in an external magnetic field, there is a force acting on it and the force experienced by the conductor is equal to the product of magnetic field, current and the length of the conductor.
$F = BIL$
The conductor B experiences force due to the magnetic field produced by the conductor A, which is given by ${B_A}$.
Therefore, the force acting on the conductor B will be equal to –
$\Rightarrow F = {B_A}{I_B}L$
Substituting the value ${B_A}$ , we have –
$\Rightarrow F = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2{I_A}{I_B}}}{d}L$
Therefore, the force per unit length between two parallel conductors is given by the expression:
$\Rightarrow f = \dfrac{F}{L} = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2{I_A}{I_B}}}{d}$
The direction of the force can be calculated by using the Fleming’s Left Hand rule where:
i) Index finger represents the direction of the magnetic field, B
ii) Middle finger represents the direction of the current, I
iii) Thumb represents the direction of the force, F
The direction of the force is represented in the diagram below:

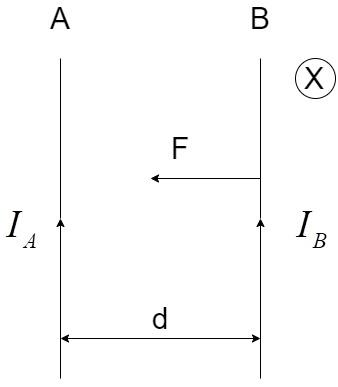
Here, the direction of ${B_A}$is calculated by the Right-Hand screw rule, which gives the result that the direction of the magnetic field is inside the plane of paper and denoted by X.

Note: The standard definition of the SI unit of current, ampere is defined by the help of the derived expression as follows:
If ${I_A} = {I_B} = 1A$ and $d = 1m$, we have –
$\Rightarrow f = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2{I_A}{I_B}}}{d} = {10^{ - 7}} \times \dfrac{{2 \times 1 \times 1}}{1} = 2 \times {10^{ - 7}}N$
Thus, One ampere is defined as the steady current, which when maintained between two infinitely long conductors with unit separation, would produce a force per unit length equal to $2 \times {10^{ - 7}}N$.