Question

Derive the formula for the volume of the frustum of a cone.

Answer 1

Hint: A cone is a three-dimensional geometric shape that tapers smoothly from a flat base to a point called the apex or vertex and its volume is given by, $\dfrac{1}{3}\pi {r^2}h$
While, a frustum is the portion of a solid that lies between one or two parallel planes cutting.
A right frustum is a parallel truncation of a right pyramid or right cone. So to solve this particular question we just have to subtract the volume of a smaller portion of the cone from the whole volume of the cone.

Complete step-by-step answer:
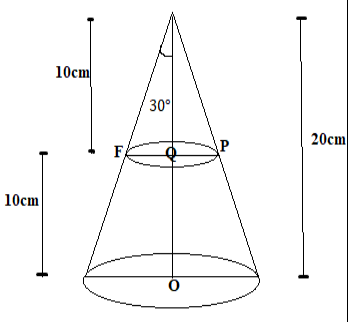
In order to solve the question, let us mark all the edges and points of cone for our simplicity as shown below,

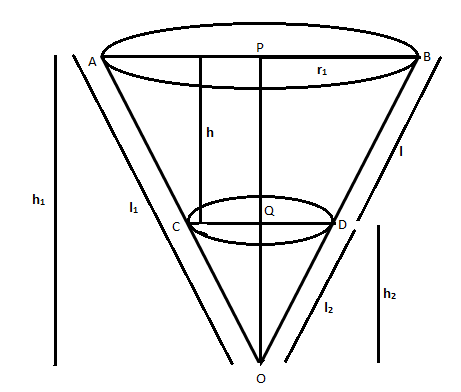
There are two cones \[OCD\]&\[OAB\],
We are given
Height of frustum \[ = h\]
Slant height of frustum \[ = l\]
Radius \[PB = {\text{ }}{r_1}\]
Radius \[QB = {\text{ }}{r_2}\]
We need to find
Curved Surface Area and Total surface Area
Here,
We need to write \[\;{h_1},{\text{ }}{l_1},{\text{ }}{h_2},{\text{ }}{l_2}\] in terms of \[h\] and \[l\]
Volume of frustum = Volume of cone OAB - Volume of cone OCD \[ = \dfrac{1}{3}\pi {r_1}^2{h_1} - \dfrac{1}{3}\pi {r_2}^2{h_{^2}}....(1)\]\[\Delta {\text{OPB & }}\Delta {\text{OQD}}\]
\[\angle BOP = \angle DOQ\] (Common)
\[\angle OPB = \angle OQD\] (Both are \[{90^o}\] as heights are perpendicular)
\[{\text{So, }}\Delta {\text{OPB ~ }}\Delta {\text{OQD}}\]
\[\therefore {\text{ }}\dfrac{{{\text{PB}}}}{{{\text{QD}}}}{\text{ = }}\dfrac{{{\text{OB}}}}{{{\text{OD}}}}\]
Since, Corresponding sides of similar triangles are proportional
\[\therefore {\text{ }}\dfrac{{{r_1}}}{{{r_2}}} = \dfrac{{{h_1}}}{{{h_2}}}\]
Putting, \[{h_1} = h + {h_2}\]
\[\dfrac{{{r_1}}}{{{r_2}}} = \dfrac{{h + {h_2}}}{{{h_2}}}\]
We split the RHS we get,
\[\dfrac{{{r_1}}}{{{r_2}}} = \dfrac{h}{{{h_2}}} + \dfrac{{{h_2}}}{{{h_2}}}\]
On cancel the term we get,
\[\dfrac{{{r_1}}}{{{r_2}}} = \dfrac{h}{{{h_2}}} + 1\]
Taking 1 on RHS we get,
\[\dfrac{{{r_1}}}{{{r_2}}} - 1 = \dfrac{h}{{{h_2}}}\]
Let us take LCM we get,
\[\dfrac{{{r_1} - {r_2}}}{{{r_2}}} = \dfrac{h}{{{h_2}}}\]
We can take a cross multiplication we get,
\[{h_2}\left( {\dfrac{{{r_1} - {r_2}}}{{{r_2}}}} \right) = h\]
Again we do cross multiplication we get,
\[{h_2} = h\left( {\dfrac{{{r_2}}}{{{r_1} - {r_2}}}} \right)....(2)\]
From\[\left( 1 \right)\], Volume of the frustum\[ = \dfrac{1}{3}\pi {r_1}^2{h_1} - \dfrac{1}{3}\pi {r_2}^2{h_{^2}}\]
putting, \[{h_1} = h + {h_2}\]
Volume of the frustum \[{\text{ }} = \dfrac{1}{3}\pi {r_1}^2\left( {h + {h_2}} \right) - \dfrac{1}{3}\pi {r_2}^2{h_{^2}}\]
From \[\left( 2 \right)\]: Putting \[{h_2} = h\left( {\dfrac{{{r_2}}}{{{r_1} - {r_2}}}} \right)\]
\[ = \dfrac{1}{3}\pi {r_1}^2\left( {h + h\left( {\dfrac{{{r_2}}}{{{r_1} - {r_2}}}} \right)} \right) - \dfrac{1}{3}\pi {r_2}^2h\left( {\dfrac{{{r_2}}}{{{r_1} - {r_2}}}} \right)\]
Taking h as common on the terms we get,
\[ = \dfrac{1}{3}\pi {r_1}^2h\left( {1 + \left( {\dfrac{{{r_2}}}{{{r_1} - {r_2}}}} \right)} \right) - \dfrac{1}{3}\pi {r_2}^2h\left( {\dfrac{{{r_2}}}{{{r_1} - {r_2}}}} \right)\]
Let us take the LCM of the first term we get,
\[ = \dfrac{1}{3}\pi {r_1}^2h\left( {\dfrac{{{r_1} - {r_2} + {r_2}}}{{{r_1} - {r_2}}}} \right) - \dfrac{1}{3}\pi {r_2}^2h\left( {\dfrac{{{r_2}}}{{{r_1} - {r_2}}}} \right)\]
On some simplification in the numerator term we get,
\[ = \dfrac{1}{3}\pi {r_1}^2h\left( {\dfrac{{{r_1}}}{{{r_1} - {r_2}}}} \right) - \dfrac{1}{3}\pi {r_2}^2h\left( {\dfrac{{{r_2}}}{{{r_1} - {r_2}}}} \right)\]
On multiplying \[r\] terms we get,
\[ = \dfrac{1}{3}\pi h\left( {\dfrac{{{r_1}^3}}{{{r_1} - {r_2}}}} \right) - \dfrac{1}{3}\pi h\left( {\dfrac{{{r_2}^3}}{{{r_1} - {r_2}}}} \right)\]
Let us take the common terms we get,
\[ = \dfrac{1}{3}\pi h\left( {\dfrac{{{r_1}^3 - {r_2}^3}}{{{r_1} - {r_2}}}} \right)\]
Using the formula, \[{{\text{a}}^{\text{3}}}{\text{ - }}{{\text{b}}^{\text{3}}}{\text{ = (a - b)(}}{{\text{a}}^{\text{2}}}{\text{ + }}{{\text{b}}^{\text{2}}}{\text{ + ab)}}\] in the above term becomes
\[ = \dfrac{1}{3}\pi h\left( {\dfrac{{({r_1} - {r_2})({r_1}^2 + {r_2}^2 + {r_1}{r_2})}}{{{r_1} - {r_2}}}} \right)\]
On cancel the same terms we get,
\[ = \dfrac{1}{3}\pi h({r_1}^2 + {r_2}^2 + {r_1}{r_2})\]
$\therefore $ Volume of frustum=\[ = \dfrac{1}{3}\pi h({r_1}^2 + {r_2}^2 + {r_1}{r_2})\]
Hence we proved the formula for the volume of the frustum of a cone.

Note: In geometry, a frustum is the portion of a solid (normally a cone or pyramid) that lies between one or two parallel planes cutting it.
Here, we have to find the volume of the cone. Volume is the quantity of three-dimensional space enclosed by a closed surface of the frustum of a cone.
Therefore, basic knowledge about geometric shapes must be known by any student. Like in this problem, students shouldn’t be confused with whose volume is to be determined.