Question

Derive the mirror equation for a convex mirror. Using it, shows that a convex mirror always produces a virtual image, independent of the location of the object.

Answer 1

Hint: As a first step, you could make a neat ray diagram of the image formation of an object kept in front of a convex mirror. Then you could use basic geometry of similar triangles to derive the mirror equation. Then you could see how the image distance will be for a convex mirror and hence the proof for the second part.

Complete Step by step solution:
In the question, we are asked to derive the mirror equation for the case of a convex mirror. We are also asked to prove that the convex mirror produces a virtual image independent of the location of the object using the above derived relation.

As a first step, we could make a neat ray diagram of the image formation of a convex mirror.

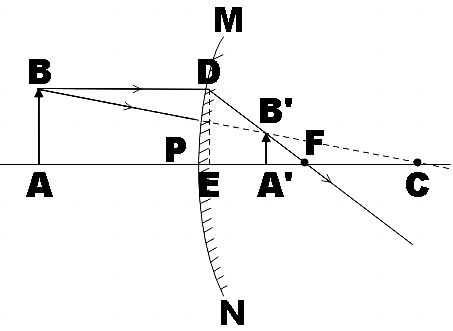
Now consider $\Delta ABC$ and $A'B'C$,
$\angle BAC=\angle B'A'C=90{}^\circ $
$\angle ACB=\angle A'CB'$
$\angle CBA=\angle CB'A'$ (common angle)

Therefore, we could say that they are similar triangles.
$\Rightarrow \dfrac{AB}{A'B'}=\dfrac{AC}{A'C}$ …………………………………….. (1)

Similarly, $\Delta DEF\sim \Delta A'B'F$
$\Rightarrow \dfrac{DE}{A'B'}=\dfrac{EF}{A'F}$ ………………………………………. (2)

When the aperture of the convex mirror is very small, $DE=AB$
Equation (2) will now become,
$\dfrac{AB}{A'B'}=\dfrac{PF}{A'F}$ …………………………………………….. (3)

From equations (1) and (3),
$\dfrac{PF}{A'F}=\dfrac{AC}{A'C}$
$\Rightarrow \dfrac{PF}{PF-PA'}=\dfrac{PA+PC}{PC-PA'}$
But we know that PF is the focal length (f), PA is the object distance (u), PA’ is the image distance (v) and PC is the radius of curvature (R=2f).
$\Rightarrow \dfrac{f}{f-v}=\dfrac{-u+2f}{2f-v}$
$\Rightarrow 2{{f}^{2}}-vf=2{{f}^{2}}-uf-2fv+uv$
$\Rightarrow fv+uf-vu=0$

Dividing each term by uvf we get,
$\dfrac{1}{u}+\dfrac{1}{v}-\dfrac{1}{f}=0$

Therefore, we derived the mirror formula for a convex lens as,
$\dfrac{1}{v}+\dfrac{1}{u}=\dfrac{1}{f}$

Now for the second part of the question, let us rearrange the formula,
$\dfrac{1}{v}=\dfrac{1}{f}-\dfrac{1}{v}$

Clearly, from the above figure, we see that the focal length of a convex mirror is always positive and object distance is always negative and thus from the above relation we see that the image distance will always be positive. This directly implies that the image will always be formed behind the mirror for an object placed anywhere in front of the convex mirror.

Note:
By convention, we take measurements from the pole of a mirror. Any measurements taken to the left of the pole are taken negative and those to the right are taken positive. Also, we have formed the image using two points:
(1) Ray parallel to principle axis passes through focal point.
(2) Ray directed towards the centre of curvature, retraces its path.