Question

Describe the construction of a compound microscope. Derive an expression for its total magnification. Draw a ray diagram for the formation of an image by a compound microscope.

Answer 1

Hint: A compound microscope is a microscope which is constructed using two convex lenses, one of the lenses is kept near the eye while the other is kept near the object that is being viewed. The image formed by the objective lens serves as an object for the ocular lens.

Formula used:
Lens formula is given as
$\dfrac{1}{f} = \dfrac{1}{v} - \dfrac{1}{u}$
where f represents the focal length, v and u represent the distance of image and object from the lens respectively.
Magnification of a lens can be calculated by the following formula:
$m = \dfrac{{h'}}{h} = \dfrac{{\text{v}}}{u}$
where h is the height of the object and u denotes the distance of the object from the lens while h’ is the height of the image of object and v denotes the distance of the image from the lens.
The total magnification due to objective lens and the eyepiece of compound microscope is given as
$m = {m_o}{m_e}$
where ${m_o}$ is the magnification due to the objective lens and ${m_e}$ is magnification due to the eye-piece.

Complete step by step answer:
A compound microscope can be constructed in the following way:
We have two convex lenses; one of the lenses is the objective lens that is kept near the object that is being viewed while the other lens is called the ocular lens or eyepiece which means that it is kept near the eye of the viewer. The image of the object formed by the objective lens is real, inverted and magnified. This image acts as an object for the second lens which forms an enlarged image which is virtual in nature. The image formed by the second lens is inverted with respect to the object and enlarged further.

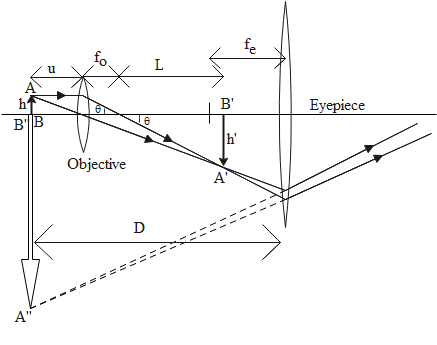
Now we can calculate the magnification due to the objective lens as follows:
${m_o} = \dfrac{{h'}}{h}$
In the figure we notice that $\tan \theta = \dfrac{h}{{{f_0}}} = \dfrac{{h'}}{L}{\text{ }} \Rightarrow \dfrac{{h'}}{h} = \dfrac{L}{{{f_0}}}$. Using this, we get
${m_o} = \dfrac{L}{{{f_0}}}$
Now magnification due to eye piece is given as
${m_e} = \dfrac{D}{{{u_e}}} = 1 + \dfrac{D}{{{f_e}}}$ (Here we have used the lens formula)
Now the total magnification is given as
$m = {m_o}{m_e} = \left( {\dfrac{L}{{{f_0}}}} \right)\left( {1 + \dfrac{D}{{{f_e}}}} \right)$
This is the required magnification.

Note: In the final expression for magnification we notice that we have the focal lengths in the denominator. This implies that in order to obtain large magnification from the compound microscope, the focal lengths of the two lenses must be small.