Question

Describe the J.J Thomson method for determining the specific charge of an electron.

Answer 1

Hint: JJ Thompson conducted an experiment to find out the electron, he did this by setting up an apparatus in which the two electrodes generate an electron which is then manipulated by the applied electric and magnetic field.

Complete solution:
As per the diagram given below, the cathode anode is connected with a battery and there is a hole in the middle of the anode. The electron will emit from the cathode and goes towards the anode with some of the electrons passing through the anode. There are two deflection coils which are also connected with a battery, the deflection coil provides an electric field between them. The electrons are passed through the coils and since the electrons have a negative charge and they move away from the electric field they get deflected from the coils. After getting deflected they strike on a sheet which is made up of a fluorescent material and glows when the electron strikes the sheet.

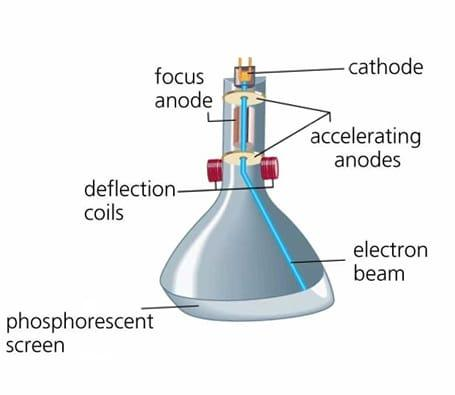
Now, at the same place where the deflecting coils are placed there is a magnetic field introduced in the area by the help of a magnet. The magnetic field is perpendicular to the electric field and puts an opposite force on the electrons. The force applied by the magnetic field is based on its strength. The strength of the magnetic field is increased till the net force on the electron comes to zero. In other words the electrons travel in a straight horizontal line or are perpendicular to both the fields.
The magnitude of the Electric field is given by:
$Ee = evB$;…(Here: Ee = Electric Field; evB = Magnetic Field)
Here,
E = Electric Field;
e = electron;
v = velocity of the electron;
B = Magnetic field;
Now, cancel out the common in the above expression:
$ \Rightarrow E = vB$;
Write the above equation in terms of v:
\[ \Rightarrow \dfrac{E}{B} = v\];
Now, let the horizontal distance travelled by the electrons after applying both Electric and Magnetic fields be x. So, by applying the speed distance formula we can find out the distance covered:
$x = vt$;
$\Rightarrow \dfrac{x}{v} = t$;
Now, the electron also moves in a vertical direction when there is no magnetic field applied and the electron is deflected after applying the electric field. Let the deflection in the vertical direction be y.
Apply Newton’s second law of motion and find out the acceleration:
$F = ma$;
$ \Rightarrow \dfrac{F}{m} = a$;
Here the force is electric force so:
$ \Rightarrow \dfrac{{eE}}{m} = a$;….(F = eE)
Now, we can apply the equation of kinematics for the deflection of electron due to electric field:
$\Rightarrow y = ut + \dfrac{1}{2}a{t^2}$;
Here, we need to note that there is no vertical displacement before the electrons gets deflected so, the initial velocity would be zero:
$\Rightarrow y = \dfrac{1}{2}a{t^2}$;
Put the value of acceleration in the above equation:
\[\Rightarrow y = \dfrac{1}{2} \times \dfrac{{eE}}{m} \times {t^2}\];
Now, put the value of time in the above equation:
\[\Rightarrow y = \dfrac{1}{2} \times \dfrac{{eE}}{m} \times \dfrac{{{x^2}}}{{{v^2}}}\];
\[ \Rightarrow y = \dfrac{1}{2} \times \dfrac{e}{m} \times E \times \dfrac{{{x^2}}}{{{v^2}}}\];
Here, \[\Rightarrow \dfrac{e}{m}\]is the specific charge which is required:
\[\Rightarrow \dfrac{{2y{v^2}}}{{E \cdot {x^2}}} = \dfrac{e}{m}\];
Now, put the value of v as \[\dfrac{E}{B} = v\]in the above equation:
\[\Rightarrow \dfrac{{2 \cdot y \cdot {E^2}}}{{E \cdot {x^2} \cdot {B^2}}} = \dfrac{e}{m}\];
Cancel out the common term:
\[ \Rightarrow \dfrac{{2 \cdot y \cdot E}}{{{x^2} \cdot {B^2}}} = \dfrac{e}{m}\];
Now, since JJ Thompson has conducted this experiment, all the value on the LHS are known, if one put the value in the above equation, on will get the value of specific charge which is:
$\Rightarrow \dfrac{e}{m} = 1.75882 \times {10^{11}}ck{g^{ - 1}}$;

The J.J Thomson method for determining the specific charge of an electron has been described above.

Note: The process is very lengthy go step by step, explain the step up first then explain the process of electron deflection after that explain how it is rectified by introducing magnetic field. Write the two equations for deflection in x axis and y axis. Relate the two equations, for finding out the acceleration apply Newton's second law of motion and put in the equation.