Question

Determine p and q such that the prime factor of 2520 is ${2^3} \times {3^p} \times q \times 7$.

Answer 1

Hint: Factors of a number can be obtained by evenly dividing the number by a series of prime factors until we obtain the quotient of 1 and remainder of 0. Series of prime factors is 2,3,5,7,11,13,17,19,23,29. So start dividing the given number by prime numbers until we obtain a quotient of 1 and remainder of 0. Then the number can be represented by multiplying all prime factors and representing it in exponential form. By comparing ${2^3} \times {3^p} \times q \times 7$ with exponential form, we can get the value of p and q.

Complete step-by-step answer:
Here the given number is 2520.
Let's start dividing the number 2520 by first prime number 2.
$\dfrac{{2520}}{2} = 1260$. Here the reminder is 0. So 2 is the first factor of 2520.
Now $\dfrac{{1260}}{2} = 630$. Here the reminder is 0. So 2 is the second factor of 2520.
Now $\dfrac{{630}}{2} = 315$. Here the reminder is 0. So 2 is the third factor of 2520.
Now $\dfrac{{315}}{2} = 157.5$. Here 315 is not evenly divided by 2. There is a reminder of 1. So 2 will not be the factor now.
Now trying with next prime number 3.
$\dfrac{{315}}{3} = 105$. Here the reminder is 0. So 3 is the fourth factor of 2520.
Now $\dfrac{{105}}{3} = 35$. Here the reminder is 0. So 3 is the fifth factor of 2520.
Now $\dfrac{{35}}{3} = 11.67$. Here 35 is not evenly divided by 3. There is a reminder of 2. So 3 will not be the factor now.
Now trying with next prime number 5.
$\dfrac{{35}}{5} = 7$. Here the reminder is 0. So 5 is the sixth prime factor of 2520.
Now $\dfrac{7}{5} = 1.4$. Here 7 is not evenly divided by 5. There is a reminder of 2. So 5 will not be the factor now.
Now trying with next prime number 7.
$\dfrac{7}{7} = 1$. Here reminder is 0 and quotient is 1. So 7 is the seventh factor of 2520.
So number 2520 can be represented by multiplying all prime factors of numbers.
So $2520 = 2 \times 2 \times 2 \times 3 \times 3 \times 5 \times 7$. It can also represented in exponential form as ${2^3} \times {3^2} \times {5^1} \times {7^1}$
So comparing ${2^3} \times {3^p} \times q \times 7$ with ${2^3} \times {3^2} \times {5^1} \times {7^1}$, so we can get p=2 and q=5

The value of p is 2 and the value of q is 5.

Note: There is an alternative method for getting the prime factors of a number. Prime Factorization of a number can be done by using the factor tree. First step for making a factor tree is to find a pair of factors whose product is the number. There may be different pairs of factors that we choose to begin the process. Let’s see here.

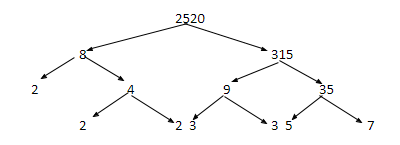
So, $2520 = 2 \times 2 \times 2 \times 3 \times 3 \times 5 \times 7$.