Question

How do you determine the amplitude period, horizontal shift and vertical shift of the function
\[8\text{ }\text{ }sin\text{ }(3x\text{ }+\pi )\text{ }-1\]?

Answer 1

Hint: In order to find the amplitude period, horizontal shift and vertical shift of any function, first we have to find whether the given equation can be expressed in terms of a trigonometric function. Then, we have to use the equation for the corresponding function. After that, we have to equate the terms of the function to obtain the respective values.

Complete answer:
The given function is
\[8\text{ }\text{ }sin\text{ }(3x\text{ }+\pi )\text{ }-1\]
We need to find
The amplitude period
The horizontal shift
And
The vertical shift of this function
Let us take
\[y=8\text{ }\text{ }sin\text{ }(3x\text{ }+\pi )\text{ }-1\] ---- (1)
Let this be equation (1)
Equation (1) can be written as,
\[y=7\text{ }\text{ }sin\text{ }(3x\text{ }+\pi )\]---- (2)
Let this be equation (2)
The general equation for a trigonometric function is,
\[y=A\text{ }sin\text{ B}(x\text{ -C})+D\] --- (3)
Let this be equation (3)

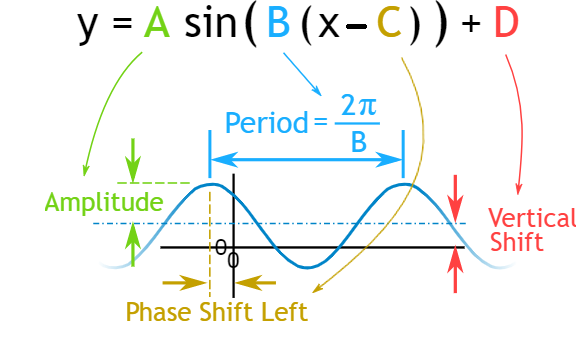
From the equation (3),
Modulus of ‘A’ is the amplitude
\[\dfrac{2\pi }{B}\] is the period
C is the horizontal phase shift
And,
D is the vertical phase shift.
By comparing equations (2) and (3),
By equating the values, we get,
\[Amplitude\text{ }=\text{ }\left| A \right|\]
Substituting the value of A, we get,
\[Amplitude\text{ }=\text{ }\left| -1 \right|\]---- (4)
Let this be equation (4)
Similarly,
The value of
\[Period=\dfrac{2\pi }{B}\]
Substituting the value of B, we get,
\[Period=\dfrac{2\pi }{3}\]--- (5)
Let this be equation (5)
Since the period is positive, it acts towards the right side.
The value of C is not given.
Therefore, horizontal phase shift will be,
\[C=0\] --- (6)
Let this be equation (6)
By comparing the value of D,
We get, vertical phase shift,
\[D=7\]--- (7)
Let this be equation (7)
Since the value of D is positive, the vertical phase shift acts upwards
Therefore, we determine the value of the amplitude period, horizontal shift and vertical shift of the function
\[8\text{ }\text{ }sin\text{ }(3x\text{ }+\pi )\text{ }-1\]as
\[Amplitude\text{ }=\text{ }\left| -1 \right|\]
\[Period=\dfrac{2\pi }{3}\]
\[Horizontal\text{ }phase\text{ }shift,\text{ }C\text{ }=\text{ }0\]
\[Vertical\text{ }phase\text{ }shift,\text{ D }=\text{ 7}\]

Note:
Both the sine and cosine functions are repetitive in nature. That is, the values of the sine and cosine functions occur repetitively in nature in a specific period of time. Such functions are referred to as periodic functions.