Question

Determine the current in each branch of the network shown in fig.

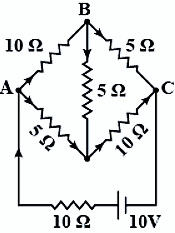
Answer 1

Hint: To solve this question, first use the formula for potential across closed circuit ABDA. But the potential across a closed circuit is zero. Substitute this value and solve the equation and obtain an equation. Similarly, find the across closed circuit BCDB, substitute the values and solve it to obtain an expression. Find the potential across the closed circuit ABCLMA, substitute the values in the equation and obtain an equation. Using all these obtained expressions, find the current in each branch of the network.

Complete solution step-by-step:

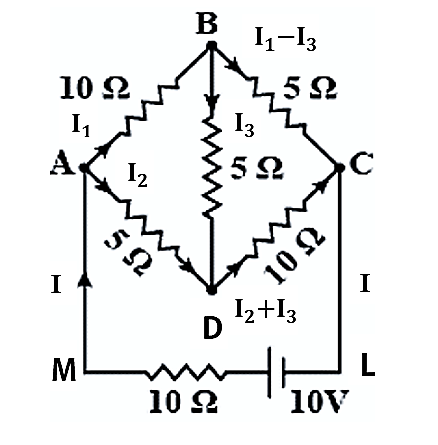
Let I be the current flowing through the outer circuit.
${I}_{1}$ be the current flowing through AB
${I}_{2}$ be the current flowing through AD
${I}_{3}$ be the current flowing through BD
${I}_{1}-{I}_{3}$ be the current flowing through BC
${I}_{2}+{I}_{3}$ be the current flowing through CD

The potential across closed circuit ABDA is given by,
${V}_{1}= 10{I}_{1}+5{I}_{3}-5{I}_{2}$ …(A)
We know, according to Kirchhoff’s law, potential across a closed circuit is zero. So, equation. (A) will be equal to zero.
$\Rightarrow 10{I}_{1}+5{I}_{3}-5{I}_{2}=0$

Dividing above equation by 5 we get,
$2{I}_{1}+{I}_{3}-{I}_{2}=0$
$\Rightarrow {I}_{2}=2{I}_{1}+{I}_{3}$ …(1)
Similarly, the potential across the closed circuit BCDB will also be equal to zero,
$5\left( { I }_{ 1 }-{ I }_{ 3 } \right) -10\left( { I }_{ 2 }+{ I }_{ 3 } \right) -5{ I }_{ 3 }=0$
Dividing above equation by 5 we get,
$\left( { I }_{ 1 }-{ I }_{ 3 } \right) -2\left( { I }_{ 2 }+{ I }_{ 3 } \right) -{ I }_{ 3 }=0$
$\Rightarrow { I }_{ 1 }-{ I }_{ 3 }-2{ I }_{ 2 }-2{ I }_{ 3 }-{ I }_{ 3 }=0$
$\Rightarrow { I }_{ 1 }-4{ I }_{ 3 }-2{ I }_{ 2 }=0$
$\Rightarrow { I }_{ 1 }= 2{I}_{2}+4{I}_{3}$ …(2)
Substituting equation. (2) in equation. (1) we get,
${ I }_{ 2 }=2\left( 2{ I }_{ 2 }+4{ I }_{ 3 } \right) +{ I }_{ 3 }$
$\Rightarrow { I }_{ 2 }= 4{ I }_{ 2 }+8{ I }_{ 3 } +{ I }_{ 3 }$
$\Rightarrow { I }_{ 2 }=4{ I }_{ 2 }+9{ I }_{ 3 }$
$\Rightarrow -3{ I }_{ 2 }=9{ I }_{ 3 }$
$\Rightarrow { I }_{ 2 }=-3{ I }_{ 3 }$ …(3)
Substituting equation. (3) in equation. (1) we get,
$-3{ I }_{ 3 }=2{ I }_{ 1 }+{ I }_{ 3 }$
$\Rightarrow -4{ I }_{ 3 }=2{ I }_{ 1 }4$
$\Rightarrow { I }_{ 1 }=-2{ I }_{ 3 }$ …(4)
The potential across the closed circuit ABCLMA will also be equal to zero.
$ -10+10I+10{ I }_{ 1 }+5\left( { I }_{ 1 }-{ I }_{ 3 } \right) =0$
Dividing above equation by 5 we get,
$ -2+2I+2{ I }_{ 1 }+ { I }_{ 1 }-{ I }_{ 3 } =0$
$\Rightarrow -2+2I+3{ I }_{ 1 }-{ I }_{ 3 }=0$
$\Rightarrow 2I+3{ I }_{ 1 }-{ I }_{ 3 }=2$ …(5)
From the above drawn figure,
$I={I}_{1}-{I}_{3}+{I}_{2}+{I}_{3}$
$\Rightarrow I={I}_{1}+{I}_{2}$ …(6)
Substituting equation. (6) in equation. (5) we get,
$2\left( { I }_{ 1 }+{ I }_{ 2 } \right) +3{ I }_{ 1 }-{ I }_{ 3 }=2$
$\Rightarrow { 2I }_{ 1 }+{ 2I }_{ 2 } +3{ I }_{ 1 }-{ I }_{ 3 }=2$
$\Rightarrow { 5I }_{ 1 }+{ 2I }_{ 2 }-{ I }_{ 3 }=2$
Substituting equation. (3) and (4) in above equation we get,
$5\left( -2{ I }_{ 3 } \right) +2\left( -3{ I }_{ 3 } \right) -{ I }_{ 3 }=2$
$\Rightarrow -10{ I }_{ 3 }-6{ I }_{ 3 }-{ I }_{ 3 }=2$
$\Rightarrow -17{ I }_{ 3 }=2$
$\Rightarrow {I}_{3}= \dfrac {-2}{17}A$ …(7)
Substituting equation. (7) in equation. (3) we get,
${ I }_{ 2 }=-3\left( \dfrac { -2 }{ 17 } \right)$
$\Rightarrow { I }_{ 2 }=\dfrac { 6 }{ 17 }A$ …(8)

Substituting equation. (7) in equation. (4) we get,
${ I }_{ 1 }=-2\left( \dfrac { -2 }{ 17 } \right)$
$\Rightarrow { I }_{ 1 }=\dfrac { 4 }{ 17 }A$ …(9)
Substituting equation. (8) and (9) in equation. (6) we get,
${I}= \dfrac {4}{17}+ \dfrac {6}{17}$
$\Rightarrow I= \dfrac {10}{17}A$

The current in branch AB is
${I}_{1}= \dfrac {4}{17}A$
The current in branch BC is
${I}_{1}-{I}_{3}= \dfrac {4}{17}- \left(\dfrac {-2}{17}\right)$
$\Rightarrow {I}_{1}-{I}_{3}= \dfrac {6}{17}$
The current in branch CD is
${I}_{2}+{I}_{3}= \dfrac {6}{17}+ \left(\dfrac {-2}{17}\right)$
$\Rightarrow {I}_{2}+{I}_{3}= \dfrac {4}{17}$
The current in branch AD is
${I}_{2}= \dfrac {6}{17}A$
The current in branch BD is
${I}_{3}= \dfrac {-2}{17}A$.

Note:
The given solution to this question is very long and has a number of equations. So, students must not get confused between them and thus, they must write the equation numbers. Students also have knowledge about Kirchhoff's law. According to Kirchhoff’s current law, the total current entering a junction is equal to the current leaving the junction. According to Kirchhoff’s voltage law, voltage around a loop is equal to the sum of every voltage drop in that loop of any closed circuit and is also equal to zero.