Question

Determine the force acting between two parallel current carrying conductor wires. Write a theoretical definition of ampere on this basis.

Answer 1

Hint: First of all, we will find out the magnetic field produced by the current in the first wire and then we will find the force experienced by the other wire due to this magnetic field in the nearby wire by making necessary substitution.

Complete step by step answer:
In the given question, we are supplied with the following data:
There are two current carrying wires, which are long and parallel.
We are required to find the force acting between the two parallel current carrying conducting wires.
To begin with, we need to first draw a diagram regarding that. The diagram contains two parallel conducting wires AB and CD, which are separated by some distance \[a\] . The wires are carrying current \[{I_1}\] and \[{I_2}\] respectively.

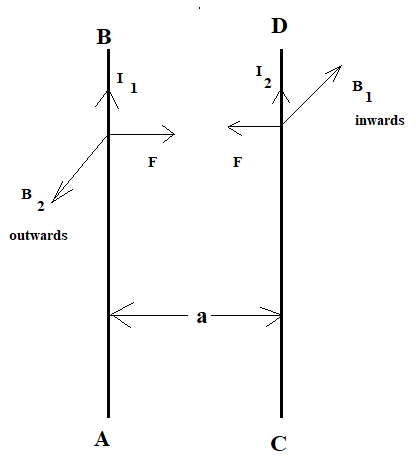
Let us proceed to solve the problem and do the derivation as we are asked.
The two conducting wires are very long.
The magnetic induction which the induced by the current in the first wire i.e. AB, due to the current \[{I_1}\] is given as:
\[{B_1} = \dfrac{{{\mu _0}{I_1}}}{{2\pi a}}\] …… (1)
Where,
\[{B_1}\] indicates the magnetic field of the first wire.
\[a\] indicates the distance of separation of the two wires.
\[{I_1}\] indicates the current flowing through the wire.
\[{\mu _0}\] indicates the permeability of free space.

The magnetic field does produce acts perpendicular to the plane of the paper and it is directed inwards. The conducting wire CD is situated in the magnetic field created by the wire AB. So, the force on the part of the wire CD due to the magnetic field present is given by:
\[F = {B_1}{I_2}l\] …… (2)
Where,
\[{B_1}\] indicates the magnetic field of the first wire.
\[{I_2}\] indicates the current flowing through the wire.
\[l\] indicates the length of the wire.

Now, we substitute the equation (1) in equation (2) and we get:
$F = {B_1}{I_2}l \\
\Rightarrow F = \dfrac{{{\mu _0}{I_1}}}{{2\pi a}} \times {I_2}l \\
\Rightarrow F = \dfrac{{{\mu _0}{I_1}{I_2}l}}{{2\pi a}} \\$
By Fleming’s left-hand rule, this force is directed towards the left.

Similarly, the magnetic induction which the induced by the current in the second wire i.e. CD, due to the current \[{I_2}\] is given as:
\[{B_2} = \dfrac{{{\mu _0}{I_2}}}{{2\pi a}}\] …… (3)
The magnetic field does produce acts perpendicular to the plane of the paper and it is directed outwards. The conducting wire AB is situated in the magnetic field created by the wire CD. So, the force on the part of the wire AB due to the magnetic field present is given by:
\[F = {B_2}{I_1}l\] …… (4)

Now, we substitute the equation (3) in equation (4) and we get:
$F = {B_2}{I_1}l \\
\Rightarrow F = \dfrac{{{\mu _0}{I_2}}}{{2\pi a}} \times {I_1}l \\
\Rightarrow F = \dfrac{{{\mu _0}{I_1}{I_2}l}}{{2\pi a}} \\$
By Fleming’s right-hand rule, this force is directed towards the right.
The two forces defined above, attract one another. Therefore, two parallel wires that carry currents in the same direction attract each other and repel each other if they carry currents in the opposite direction.

For the definition of ampere:
We have,
\[F = \dfrac{{{\mu _0}{I_1}{I_2}l}}{{2\pi a}}\]
\[\dfrac{F}{l} = \dfrac{{{\mu _0}{I_1}{I_2}}}{{2\pi a}}\] ….. (5)
Where,
\[\dfrac{F}{l}\] indicates force per unit length of the conducting wire present.
Let us take both the current as \[1\,{\text{A}}\] and the distance between the two conductors as \[1\,{\text{m}}\] .
Now the equation (5) becomes:
$\dfrac{F}{l} = \dfrac{{{\mu _0}{I_1}{I_2}}}{{2\pi a}} \\$
$\Rightarrow \dfrac{F}{l} = \dfrac{{{\mu _0}}}{{2\pi }} \times \dfrac{{1 \times 1}}{1} \\$
$\Rightarrow \dfrac{F}{l} = \dfrac{{4\pi \times 1{0^{ - 7}}}}{{2\pi }} \\$
$\Rightarrow \dfrac{F}{l} = 2 \times 1{0^{ - 7}}{\text{N}}\,{{\text{m}}^{ - 1}} \\$
Ampere is defined as the constant current that experiences a force of \[2 \times 1{0^{ - 7}}\] Newton per unit length of the conductor when flowing through two parallel, infinitely long straight conductors of negligible cross section and placed in air or vacuum at a distance of one metre apart.

Note:
While solving this problem, it is important to remember that the force on one wire is due to the magnetic field of the other wire. Most of the students tend to make mistakes by taking its own magnetic field into account while calculating force on that particular wire. If the currents are moving in the same direction the force attracts and if the currents are moving in the opposite direction then the force repels.