Question

Determine the value of $\sec ( - {45^\circ })$
${\text{(A) }}\sqrt {\text{2}} $
${\text{(B) - }}\sqrt {\text{2}} $
${\text{(C) }}\sqrt 1 $
${\text{(D) - }}\sqrt 1 $

Answer 1

Hint: First we must convert the negative angle to positive angle. We will first see where the specific angle lies in the angle graph and then use the appropriate formula to calculate the value.

Formula used: $\sec (\theta ) = \dfrac{1}{{\cos (\theta )}}$
$\cos (A + B) = \cos A\cos B - \operatorname{Sin} A\operatorname{Sin} B$

Complete step-by-step answer:
We know that \[\sec (\theta ) = \dfrac{1}{{\cos (\theta )}}\]
So we have to put the value of \[\theta \]
$\Rightarrow$$\sec ( - 45^\circ ) = \dfrac{1}{{\cos ( - 45^\circ )}}$

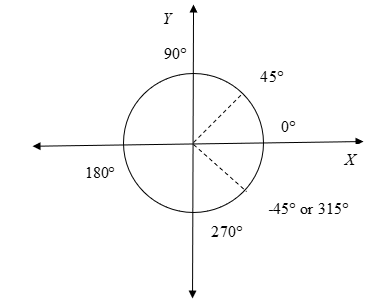
From the graph we can see that the angle $ - {45^ \circ }$ corresponds to angle $315^\circ $.
Therefore, angle $315^\circ $ can be written as a combination of $270^\circ + 45^\circ $
Therefore, the question can be rewritten as:
$\Rightarrow$$\sec (315^\circ ) = \dfrac{1}{{\cos (315^\circ )}}$
This could further be written as:
$\Rightarrow$$\sec (270^\circ + 45^\circ ) = \dfrac{1}{{\cos (270^\circ + 45^\circ )}} ………………. (1)$
Now let’s consider $\cos (270^\circ + 45^\circ )$
We know that $\cos (A + B) = \cos A\cos B - \operatorname{Sin} A\operatorname{Sin} B$
Therefore, the problem could be expanded as:
$\Rightarrow$$\cos (270^\circ + 45^\circ ) = \cos (270^\circ )\cos (45^\circ ) - \sin (270^\circ )\sin (45^\circ )$
Now from the trigonometric table that:
$\cos (270^\circ ) = 0$,
$\cos (45^\circ ) = \dfrac{1}{{\sqrt 2 }}$,
$\sin (270^\circ ) = - 1$,
$\sin (45^\circ ) = \dfrac{1}{{\sqrt 2 }}$.
On substituting the values, we get:
$\Rightarrow$$\cos (270^\circ + 45^\circ ) = 0 \times \dfrac{1}{{\sqrt 2 }} - ( - 1) \times \dfrac{1}{{\sqrt 2 }}$
On simplifying we get:
$\Rightarrow$$\cos (270^\circ + 45^\circ ) = \dfrac{1}{{\sqrt 2 }}.................\left( 2 \right)$
Now on substituting the value $\left( 2 \right)$ in equation $(1)$we get:
$\Rightarrow$$\sec (270^\circ + 45^\circ ) = \dfrac{1}{{\dfrac{1}{{\sqrt 2 }}}}$
On simplifying we get:
$\Rightarrow$$\sec (270^\circ + 45^\circ ) = \sqrt 2 $
Hence $\sec ( - {45^\circ }) = \sqrt 2 $ is the required answer.

$\therefore $The correct answer is option $(A)$.

Note: A negative angle is an angle which is traced clockwise from $0^\circ $, therefore at that same point when traced anti-clockwise, would be another angle which is the same angle but positive.
In these types of questions, the various trigonometric formulas should be remembered such as the angle formulas and the sum and difference identities should also be remembered.
A graph should be made to visualize the angle on which the calculation is to be made.
There directly won’t be sum and difference identities for ${\text{sec\theta , cosec\theta or cot\theta }}$ so therefore they should be converted into their respective identities and the formulas should be then applied. Thereafter it should not be forgotten to convert the solution back to the original format because not converting it would result in an incomplete answer.