
How do you determine the vertex as an ordered pair when $f\left( x \right) = 3{\left( {x + 2} \right)^2} - 1$?
Answer
438k+ views
Hint: The equation in the question represents a parabola and we have to find the vertex of the given parabola equation, and to find the vertex of the parabola, we should know that the equation of the vertex form is \[y = a{\left( {x - h} \right)^2} + k\], where \[\left( {h,k} \right)\] is the vertex of the parabola, now compare the two equations and we will get the required vertex.
Complete step by step solution:
Given the equation is $f\left( x \right) = 3{\left( {x + 2} \right)^2} - 1$, from the equation we are given that the equation represents a parabola and the parabola does not pass through the origin.
Let us take $y = f\left( x \right) = 3{\left( {x + 2} \right)^2} - 1$,
We can say that,
$y = 3{\left( {x + 2} \right)^2} - 1$,
Now to find the vertex of the parabola,
We know that the equation of parabola in the vertex form can be written as \[y = a{\left( {x - h} \right)^2} + k\], where\[\left( {h,k} \right)\]is the vertex of the parabola,
So here the equation is $f\left( x \right) = 3{\left( {x + 2} \right)^2} - 1$,
Now comparing the two equations we get , \[a = 3\],\[h = - 2\] and \[k = - 1\]
So the vertex of the parabola is \[\left( { - 2, - 1} \right)\],
If we plot the parabola, we get the graph as,
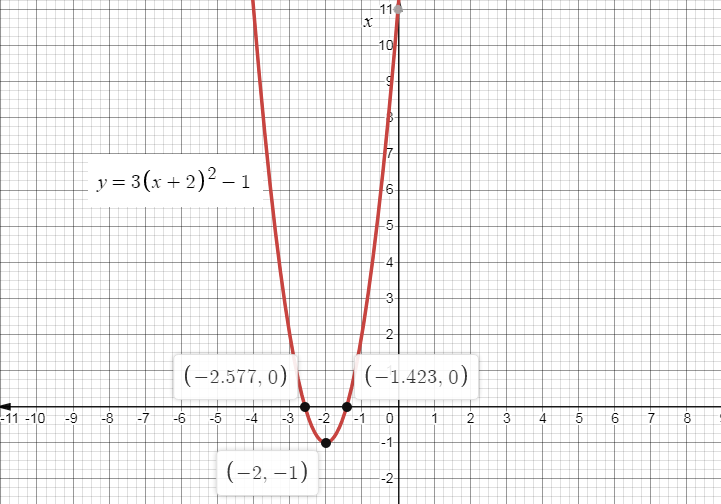
Final Answer:
\[\therefore \] The vertex of the parabola $f \left( x \right) = 3{\left( {x + 2} \right)^2} - 1$ will be equal to \[\left( { - 2, - 1} \right)\], and the graph will be
Note: Symmetric points are called the points which are equidistant from the axis of symmetry and lie on the \[x\]-axis and they are calculated as \[x\]-intercepts. To find the vertex of the parabola we can also make use of the standard form of the equation \[y = a{x^2} + bx + c\], where the axis of symmetry or the \[x\]-coordinate is given by \[x = \dfrac{{ - b}}{{2a}}\] and then we will find the value of \[y\]from the equation of the parabola.
Complete step by step solution:
Given the equation is $f\left( x \right) = 3{\left( {x + 2} \right)^2} - 1$, from the equation we are given that the equation represents a parabola and the parabola does not pass through the origin.
Let us take $y = f\left( x \right) = 3{\left( {x + 2} \right)^2} - 1$,
We can say that,
$y = 3{\left( {x + 2} \right)^2} - 1$,
Now to find the vertex of the parabola,
We know that the equation of parabola in the vertex form can be written as \[y = a{\left( {x - h} \right)^2} + k\], where\[\left( {h,k} \right)\]is the vertex of the parabola,
So here the equation is $f\left( x \right) = 3{\left( {x + 2} \right)^2} - 1$,
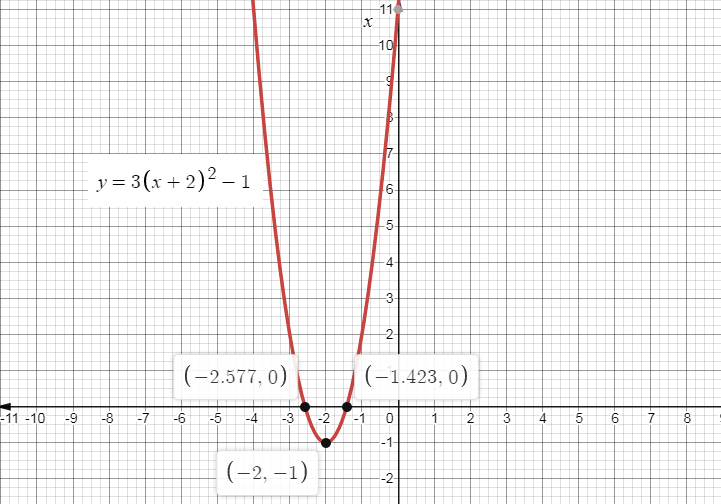
Now comparing the two equations we get , \[a = 3\],\[h = - 2\] and \[k = - 1\]
So the vertex of the parabola is \[\left( { - 2, - 1} \right)\],
If we plot the parabola, we get the graph as,

Final Answer:
\[\therefore \] The vertex of the parabola $f \left( x \right) = 3{\left( {x + 2} \right)^2} - 1$ will be equal to \[\left( { - 2, - 1} \right)\], and the graph will be

Note: Symmetric points are called the points which are equidistant from the axis of symmetry and lie on the \[x\]-axis and they are calculated as \[x\]-intercepts. To find the vertex of the parabola we can also make use of the standard form of the equation \[y = a{x^2} + bx + c\], where the axis of symmetry or the \[x\]-coordinate is given by \[x = \dfrac{{ - b}}{{2a}}\] and then we will find the value of \[y\]from the equation of the parabola.
Recently Updated Pages
Master Class 11 Accountancy: Engaging Questions & Answers for Success

Express the following as a fraction and simplify a class 7 maths CBSE

The length and width of a rectangle are in ratio of class 7 maths CBSE

The ratio of the income to the expenditure of a family class 7 maths CBSE

How do you write 025 million in scientific notatio class 7 maths CBSE

How do you convert 295 meters per second to kilometers class 7 maths CBSE

Trending doubts
10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

State and prove Bernoullis theorem class 11 physics CBSE

What organs are located on the left side of your body class 11 biology CBSE

Write down 5 differences between Ntype and Ptype s class 11 physics CBSE




