Question

Diagonal of a rectangle is 25 cm and the length of the rectangle is 20 cm. Find the area of the rectangle.

Answer 1

Hint: We will use the Pythagoras theorem to solve this question for the value of breadth of the rectangle with the diagonal and length of the rectangle provided in the question. Once we have calculated the value of the breadth, we will use the formula of the area of the rectangle as: Area of the rectangle = length of the rectangle $ \times $ breadth of the rectangle.

Complete step-by-step answer:
We are given a rectangle whose length is 20 cm and diagonal = 25 cm.
Let us draw a figure of the rectangle:

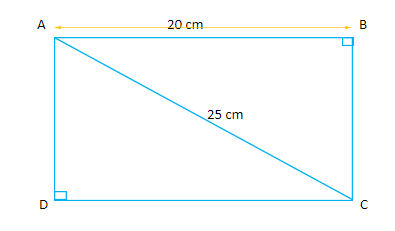
Let ABCD be a rectangle and AC be one of the diagonals of the rectangle. As we know that $\angle $ABC is 90°, therefore $\vartriangle ABC$ is a right – angled triangle.
Using the Pythagoras theorem in the $\vartriangle ABC$ to calculate the value of the breadth of the rectangle, we get
$ \Rightarrow A{C^2} = A{B^2} + B{C^2}$
On putting the values of the diagonal and length of the rectangle, we get
$
   \Rightarrow {25^2} = {20^2} + B{C^2} \\
   \Rightarrow 625 = 400 + B{C^2} \\
   \Rightarrow B{C^2} = 625 - 400 \\
   \Rightarrow B{C^2} = 225 \\
   \Rightarrow BC = \sqrt {225} = 15 \\
 $
Therefore, the breadth of the rectangle is 15 cm.
Now, we know that the formula of the area of the rectangle is given by:
Area of the rectangle = length of the rectangle $ \times $ breadth of the rectangle.
$ \Rightarrow $Area of the rectangle = 20$ \times $15 = 300 $cm^2$.


Note: In such questions, you may get confused while calculating the breadth of the rectangle with length and the diagonal given. As one angle is 90°so we are using the Pythagoras theorem in this question.