Question

What is the difference between $2\cos x$ and $\cos 2x$?

Answer 1

Hint: In the function $2\cos x$ the cosine term is doubled, while in the function $\cos 2x$, the argument of the cosine function will get doubled. The difference between the two functions will get reflected in their ranges. The range of the cosine function, which is a sinusoidal function, is equal to \[\left[ -1,1 \right]\]. From this range, we can obtain the ranges of both the given functions.

Complete step by step solution:
The trigonometric functions given in the above question are $2\cos x$ and $\cos 2x$. Let us consider these trigonometric functions as
\[\begin{align}
  & \Rightarrow y=\cos 2x......\left( i \right) \\
 & \Rightarrow y=2\cos x......\left( ii \right) \\
\end{align}\]
We can see that both the functions are expressed in terms of the cosine function. The difference between the two is in the first function, the argument is doubled, while in the second function, the cosine of the argument x is doubled.
We know that the cosine is a sinusoidal function whose value varies from $-1$ to $1$. Therefore, the range of the function represented in the equation (i) will be equal to \[\left[ -1,1 \right]\].
In the function represented in the equation (ii), since the cosine term, whose value varies from $-1$ to $1$ is doubled, its range will be given by
$\begin{align}
  & \Rightarrow 2\left[ -1,1 \right] \\
 & \Rightarrow \left[ -2,2 \right] \\
\end{align}$
Thus, the range of the function $2\cos x$ is equal to \[\left[ -2,2 \right]\].
We can interpret the difference in the two functions by their graphs given below.

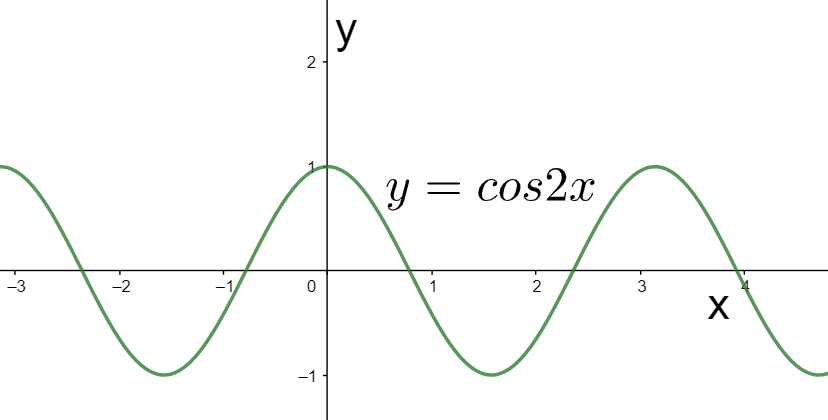
Note: From the graph of the two functions in the above solution we can appreciate that the difference is not only in their ranges, but their periods too. The period of the first function $\cos 2x$ is half of that of the second function $2\cos x$. We can also show the difference between the given functions by considering the function of their difference, that is, $y=\cos 2x-2\cos x$. We can simplify this function using the trigonometric identity $\cos 2x=2{{\cos }^{2}}x-1$ so that the function gets simplified to $y=2{{\cos }^{2}}x-2\cos x-1$.