Question

What is the difference between x – intercepts, zeros and roots?

Answer 1

Hint: For solving this question you should know about the x – intercepts of a line and the zeros and roots of a polynomial. The x – intercept of a line or graph is the point where the line cuts to the x – axis and this point is known as intercept point. And the zeros and roots both are the same.

Complete step-by-step answer:
According to our questions we have to distinguish between x – intercepts, zeros and roots.
So, as we know that the line is always in the form of \[y=mx+c\] and if we make any line which cuts to the x – axis and y -axis. Then the points where the line cuts to both those points are respectively known as the x – intercept point and y – intercept point. And both will always be different from one another.
If we take an example then we can understand it smoothly.
Eg. (1) Determine the x and y – intercepts of the line - \[y=\dfrac{1}{2}x-3\].
For solving this we will determine the values of y at different points of x.
So, if we take \[x=6\]
\[y=\dfrac{1}{2}\left( 6 \right)-3=3-3=0\]
The point is (6, 0).
And if we take \[x=0\]
Then \[y=0-3=-3\]
The point is (0, -3)
If we make graph for this:

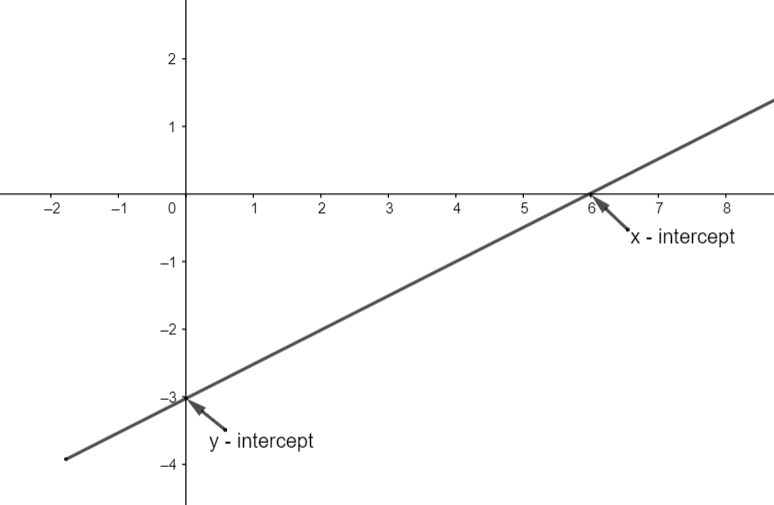
x – intercept is (6, 0)
and y – intercept is (0, -3)
The zeros and roots are the same. And the zeros and roots of a functions f is a value \[{{x}_{0}}\] at which \[f\left( {{x}_{0}} \right)\] will be equal to zero.
It means roots or zero of a function \[f\left( x \right)\] is \[x={{x}_{0}}\] if \[f\left( {{x}_{0}} \right)=0\].
Then \[{{x}_{0}}\] will be a root for this.
And the x – intercepts are equal to zeros and roots of \[y=f\left( x \right)\], if the x – intercepts are the points at which \[y=0\] means the appear exactly at \[f\left( x \right)=0\], i.e., where x is a root of the function.
Here, the root of the \[y=\dfrac{1}{2}x-3\] is x – intercept which is 6.
At this point y = 0.

Note: For calculating the intercepts of any function we plot it on a graph or we can also calculate by the general form of that function and satisfy that at random points. But the roots of a function will be equal to x – intercept if the \[y=0\] at that value of x. Then the value of x will be a root for this.