Question

Differentiate between consistent and inconsistent systems. Define angles of elevation and depression.

Answer 1

Hint: To differentiate between consistent and inconsistent systems we can use either numerical way or graphical way. In graphical way, if graphs of given lines meet or intersect somewhere. Then lines are said to be consistent. But, if the graph of lines do not meet anywhere in the plane. Then lines are said to be inconsistent.
In numerical way there are two formulas. If lines satisfy condition $\dfrac{{{a_1}}}{{{a_2}}} \ne \dfrac{{{b_1}}}{{{b_2}}}$then liens will be consistent and if they satisfy condition$\dfrac{{{a_1}}}{{{a_2}}} = \dfrac{{{b_1}}}{{{b_2}}} \ne \dfrac{{{c_1}}}{{{c_2}}}$. Then lines will be inconsistent.

Complete step by step solution:
Let a pair of linear equations in two variable as:
\[{a_1}x + {b_1}y + {c_1} = 0\] and
\[{a_2}x + {b_2}y + {c_2} = 0\]
We can find the solution to these equations by graphical or algebraic method.
Consistent system
By drawing the graph of these two lines, following cases are possible:
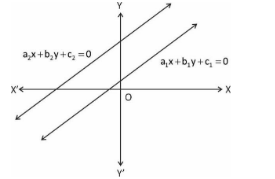
(i) If both the lines intersect at a point, then there exists a unique solution to the pair of linear equations. So the pair of linear equations is said to be consistent
Lines intersect at point \[P\left( {x,\,\,y} \right)\]
Point P(x, y) represent unique solution
Algebraically, if \[\dfrac{{{a_1}}}{{{a_2}}}\,\, \ne \,\,\dfrac{{{b_1}}}{{{b_2}}}\] the linear equation is consistent.

(ii) If the lines of a pair of linear equations coincide with each other, then there exist infinitely many solutions since a line consists of infinite points. The pair of linear equations said to be consistent.
Algebraically,\[\dfrac{{{a_1}}}{{{a_2}}} = \dfrac{{{b_1}}}{{{b_2}}} = \dfrac{{{c_1}}}{{{c_2}}}\]the pair of linear equation said to be consistent.

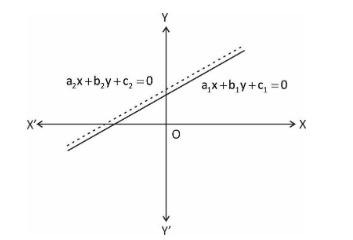
Inconsistent system
Consider the equations
\[{a_1}x + {b_1}y + {c_1} = 0\] and
\[{a_2}x + {b_2}y + {c_2} = 0\]
Let both the lines are parallel to each other, then there exist No solution because the lines never intersect

Algebraically, for such a case
\[\dfrac{{{a_1}}}{{{a_2}}} = \dfrac{{{b_1}}}{{{b_2}}} \ne \dfrac{{{c_1}}}{{{c_2}}}\]
The pair of linear equations in the variables is said to be inconsistent.

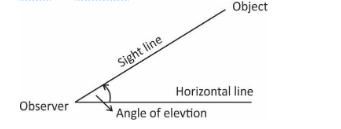
Angle of elevation:
The term angle of elevation denotes the angle from the horizontal upward to an object. An observer's line of sight would be above the horizontal.

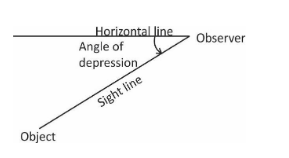
Angle of depression:
The term angle of depression denotes the angle from the horizontal downward to an object. An observer’s line of sight would be below the horizontal.

Note: The angle of elevation is when you are measuring the angle from the floor or the ground, and the angle of depression is when you are measuring from a ceiling. The only time the two angles are equal is if the ceiling and floor are parallel with each other. If you know your angle terms these are opposite interior angles.