Answer
Verified437.4k+ views
Hint:Hint: In this type of descriptive question we define the technical terms first like, Adjacent angles in this case. Then we discuss the properties of adjacent angles and elaborate its use and importance while reflecting upon the implications of it in real life.
Complete solution step by step:
We firstly define what adjacent angle is Adjacent angles: Two angles which are not overlapping and have a common vertex and a common side between the two. We can understand it in a better way by this figure-
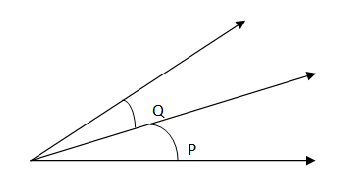
In the figure$\angle P\,{\text{and}}\,\angle Q$are adjacent angles because they share the same vertex and one side is common between the two.
These conditions should be satisfied to ensure the angles are adjacent:
1) Common side/arm
2) Common vertex
3) No overlapping of the two angles
4) No common interior point
Mathematics is the language of nature and angles are no less prevalent in our surroundings. Angles can be seen everywhere in our life but we don’t see them with our analytical lens. Be it an opened book or a window of our house shapes, our world is full of angles.
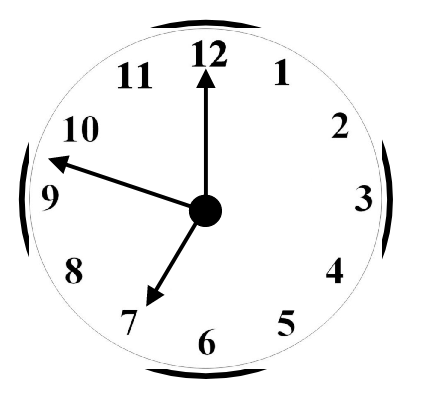
Adjacent angles can be seen and observed when we look at hands of a clock denoting different time. We need three arms to make an adjacent angle and in a clock we have three hands.
For example, when a clock shows time as 7 AM and the arm which shows seconds in a clock if it is between 7 to 12 then it makes an adjacent angle as shown below
Some other examples of adjacent angles would be - Cycle wheels, Scissors when arms are opened, Book when opened makes adjacent angles with both the covers and pages inside etc.
Notes: If the sum of two adjacent angles is $180^\circ $then they are known as linear pairs of angles. And in this case the non common arms form a line. An example of this can be a T-point on a road which makes adjacent angles at the same time a linear pair of angles.
Complete solution step by step:
We firstly define what adjacent angle is Adjacent angles: Two angles which are not overlapping and have a common vertex and a common side between the two. We can understand it in a better way by this figure-
In the figure$\angle P\,{\text{and}}\,\angle Q$are adjacent angles because they share the same vertex and one side is common between the two.
These conditions should be satisfied to ensure the angles are adjacent:
1) Common side/arm
2) Common vertex
3) No overlapping of the two angles
4) No common interior point
Mathematics is the language of nature and angles are no less prevalent in our surroundings. Angles can be seen everywhere in our life but we don’t see them with our analytical lens. Be it an opened book or a window of our house shapes, our world is full of angles.
Adjacent angles can be seen and observed when we look at hands of a clock denoting different time. We need three arms to make an adjacent angle and in a clock we have three hands.
For example, when a clock shows time as 7 AM and the arm which shows seconds in a clock if it is between 7 to 12 then it makes an adjacent angle as shown below
Some other examples of adjacent angles would be - Cycle wheels, Scissors when arms are opened, Book when opened makes adjacent angles with both the covers and pages inside etc.
Notes: If the sum of two adjacent angles is $180^\circ $then they are known as linear pairs of angles. And in this case the non common arms form a line. An example of this can be a T-point on a road which makes adjacent angles at the same time a linear pair of angles.