Question

What is the dispersive power of the prism and its SI unit?

Answer 1

Hint:The breaking of white light into its constituent colours is referred to as dispersion. A spectrum is a collection of colours. The separation of different colours of light by refraction is the dispersive power of a transparent medium.

Complete answer:
Initially, the dispersion was examined through a glass prism. It occurs because the refractive index of the medium's substance varies depending on the colour. The term "colours' ' refers to the wavelengths. The ratio of the difference in refractive index of two different wavelengths to the refractive index at some defined intermediate wavelength determines the dispersive power of any transparent medium.

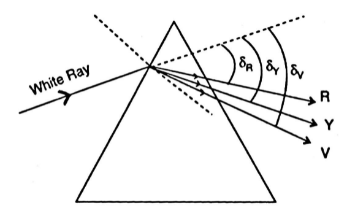
Consider a glass prism as an example; a prism's refractive index is provided by the relationship
$\mu = \dfrac{{\sin \dfrac{{A + D}}{2}}}{{\sin \dfrac{A}{2}}}$
Where $A$ is the prism angle and $D$ is the minimum deviation angle. If $A$ is a small angled prism's refractive angle and is the angle of deviation $\delta $.

The prism formula is as follows:
$\mu = \dfrac{{\sin \dfrac{{A + \delta }}{2}}}{{\sin \dfrac{A}{2}}}$
Because we're talking about small angled prisms,
$\sin \dfrac{{A + \delta }}{2} = \dfrac{{A + \delta }}{2}\,and\,\sin \dfrac{A}{2} = \dfrac{A}{2} \\
\Rightarrow \mu = \dfrac{{\dfrac{{A + \delta }}{2}}}{{\dfrac{A}{2}}} \\
\Rightarrow \mu A = A + \delta \\ $
Therefore, $\delta = \left( {\mu - 1} \right)A$
If $\delta v$ and $\delta r$ are the deviations of the violet and red rays, the corresponding wavelengths are given as $\mu v$ and $\mu r$ . So, the angular dispersion is given as
${\delta _v} - {\delta _r} = \left( {{\mu _v} - {\mu _r}} \right)A$

The angular dispersion is known as the difference in deviation between extreme colours.If $\delta y$ and $\mu y$are the deviation and refractive index of an intermediate wavelength yellow,
${\delta _y} = \left( {{\mu _y} - 1} \right)A$
On dividing both equation, we get
$\dfrac{{{\delta _v} - {\delta _r}}}{{{\delta _y}}} = \dfrac{{{\mu _v} - {\mu _r}}}{{{\mu _y}}}$
The expression $\dfrac{{{\delta _v} - {\delta _r}}}{{{\delta _y}}}$ is known as dispersive power of the material of the prism and is denoted by $\omega $.
$\therefore \omega = \dfrac{{{\mu _v} - {\mu _r}}}{{{\mu _y}}}$
The ratio of angular dispersion for any two wavelengths to the deviation of mean wavelength is the dispersive power of a prism's material.The SI unit of dispersive power is $watt$.

Note:Violet rays have a higher deviation and refractive index than red rays. As a result, violet rays travel at a slower speed through glass than red rays. Yellow rays' refractive index and deviation are used as mean values.