Question

What is the distance between the parallel lines 3x + 4y + 7 = 0 and 3x + 4y – 5 = 0?
(a). \[\dfrac{2}{5}\]
(b). \[\dfrac{{12}}{5}\]
(c). \[\dfrac{5}{{12}}\]
(d). \[\dfrac{3}{5}\]

Answer 1

Hint: The distance between two parallel lines \[ax + by + {c_1} = 0\] and \[ax + by + {c_2} = 0\] is given by the formula \[d = \dfrac{{|{c_1} - {c_2}|}}{{\sqrt {{a^2} + {b^2}} }}\]. Use this formula to find the distance between the given lines.

Complete step-by-step answer:
Two lines are said to be parallel if they do not intersect at any finite point in the space. They always maintain the same distance between them.
The equations of the parallel lines have the x and y coefficient as proportional to each other.
For finding the distance between the two parallel lines, we first express the two equations such that the coefficients of x and y are equal.
We have the equations of two lines as follows:
3x + 4y +7 = 0
3x + 4y – 5 = 0
Hence, we have both equations such that the x and y coefficients are equal.

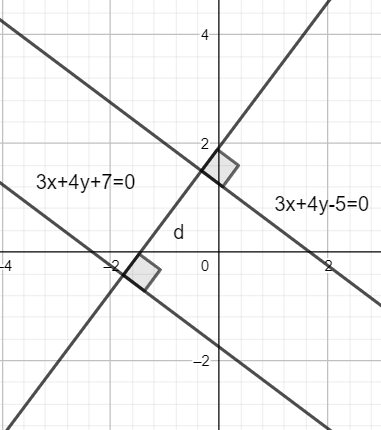
Now, we use the formula for calculating the distance between two parallel lines \[ax + by + {c_1} = 0\] and \[ax + by + {c_2} = 0\] given as follows:
\[d = \dfrac{{|{c_1} - {c_2}|}}{{\sqrt {{a^2} + {b^2}} }}\]
From the equations of the lines, we have:
\[{c_1} = 7\]
\[{c_2} = - 5\]
a = 3
b = 4
Then, we have:
\[d = \dfrac{{|7 - ( - 5)|}}{{\sqrt {{3^2} + {4^2}} }}\]
Simplifying, we have:
\[d = \dfrac{{|7 + 5|}}{{\sqrt {9 + 16} }}\]
\[d = \dfrac{{|12|}}{{\sqrt {25} }}\]
We know that the square root of 25 is 5. Hence, we have:
\[d = \dfrac{{12}}{5}\]
Hence, the correct answer is option (b).

Note: Note that you should take care of the negative sign in the equation 3x + 4y – 5 = 0 and include it while calculating the distance, otherwise, your answer will be \[\dfrac{2}{5}\], option (a), which is wrong.