
How much distance did the car cover during the period 7:30 a.m. to 8 a.m.?
A. 20 km
B. 40 km
C. 80 km
D. 100 km

Answer
579.6k+ views
Hint: We here have been given a distance time graph for a car and we need to find the distance covered by it in between the duration 7:30am to 8am. For this, we will first calculate the speed of the car which will be equal to the slope of the distance-time curve, i.e. the slope of the line. Then we will calculate the time that went by (in hours) in the given time duration. Then, we will use the formula given as:
The speed ‘v’ is given as:
$v=\dfrac{s}{t}$
Where, t=time taken
s=distance covered in t time
Then we will put the values of v and t in this equation and hence obtain the desired value of ‘s’.
Complete step by step answer:
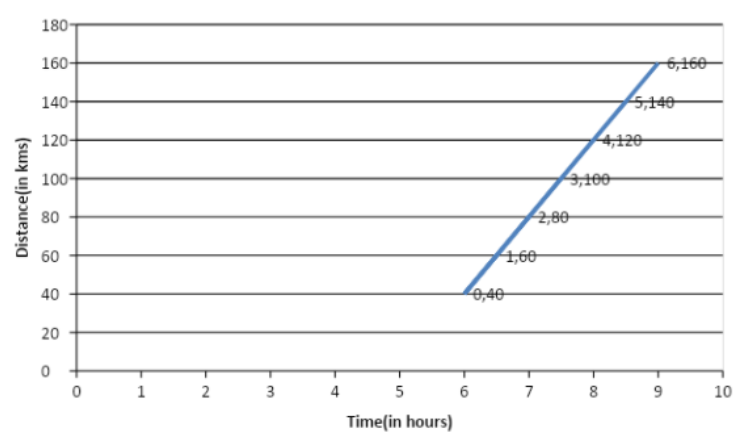
We here have been given the following graph:
And we have to find the distance covered by the car in the duration between 7:30 a.m. to 8 a.m.
For this, we will first find the speed of the car. We know that the speed of the car is equal to the slope of the distance-time curve.
Hence, if the speed of the car is ‘v’, then v is equal to:
$\begin{align}
& v=\text{slope of the line}=\dfrac{160-40}{9-6} \\
& \Rightarrow v=\dfrac{120}{3} \\
& \Rightarrow v=40km/hr \\
\end{align}$
Thus, the speed of the car is 40km/hr.
Now, the duration given to us is between 7:30 a.m. to 8 a.m.
The time covered (in hours) in this duration is given as the difference of two times as both of them are in ‘a.m.’ But before we do that, we need to change 7:30 a.m. completely into hours.
Now, we know that 7:30 is half past 7. That means half an hour has passed after 7 at 7:30.
Thus, we can write 7:30 as:
$7:30=7\dfrac{1}{2}$
Thus, the time between the given time duration is:
$\left( 8-7\dfrac{1}{2} \right)hours$
Now, we know that $7\dfrac{1}{2}=\dfrac{15}{2}$
Thus, we get the time as:
$\begin{align}
& \left( 8-7\dfrac{1}{2} \right)hours \\
& \Rightarrow \left( 8-\dfrac{15}{2} \right)hours \\
& \Rightarrow \left( \dfrac{16-15}{2} \right)hours \\
& \Rightarrow \dfrac{1}{2}hours \\
\end{align}$
Hence, the given time duration is $\dfrac{1}{2}$ hours.
Now, we know that the speed ‘v’ is given as:
$v=\dfrac{s}{t}$ …..(i)
Where, t=time taken
s=distance covered in t time.
We know that here we have:
v=40km/hr
t=$\dfrac{1}{2}$ hour
Now, if we put the values of t and v in equation (i), we will get the value of s.
Thus, putting these values in equation (i) we get:
$\begin{align}
& v=\dfrac{s}{t} \\
& \Rightarrow 40=\dfrac{s}{\dfrac{1}{2}} \\
& \Rightarrow s=40\times \dfrac{1}{2} \\
& \therefore s=20km \\
\end{align}$
Hence, the distance covered in the given duration of time is 20km.
Thus, option (A) is the correct option.
Note:
We here can also obtain the required distance covered by reading the graphs follows:
The given graph is:
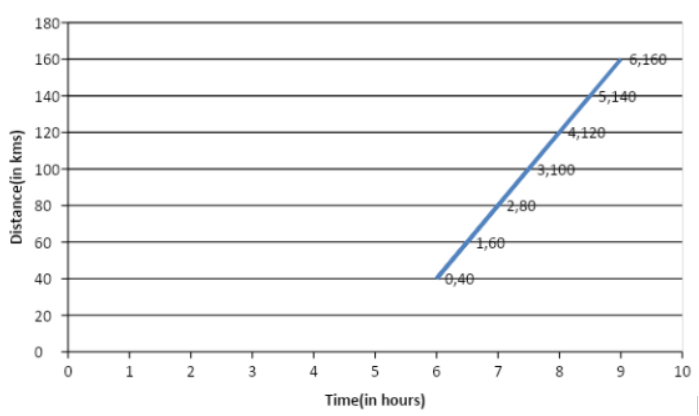
Now, if we read the graph, we can see that the car has already covered a distance of 100 km till 7:30 am.
Similarly, we can also read from the graph that the car has covered a total distance of 120km till 8am.
Hence, the distance covered in the given time duration will be the difference between the total distances that have been covered at the starting and the end points of the given duration.
Thus, the required distance is given as:
$\begin{align}
& 120-100 \\
& \therefore 20km \\
\end{align}$
The speed ‘v’ is given as:
$v=\dfrac{s}{t}$
Where, t=time taken
s=distance covered in t time
Then we will put the values of v and t in this equation and hence obtain the desired value of ‘s’.
Complete step by step answer:
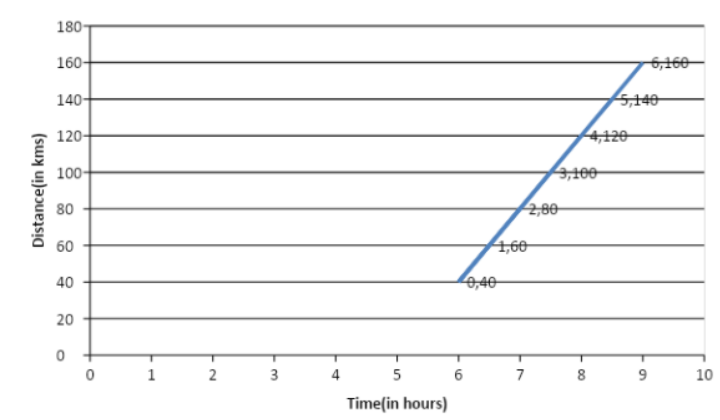
We here have been given the following graph:

And we have to find the distance covered by the car in the duration between 7:30 a.m. to 8 a.m.
For this, we will first find the speed of the car. We know that the speed of the car is equal to the slope of the distance-time curve.
Hence, if the speed of the car is ‘v’, then v is equal to:
$\begin{align}
& v=\text{slope of the line}=\dfrac{160-40}{9-6} \\
& \Rightarrow v=\dfrac{120}{3} \\
& \Rightarrow v=40km/hr \\
\end{align}$
Thus, the speed of the car is 40km/hr.
Now, the duration given to us is between 7:30 a.m. to 8 a.m.
The time covered (in hours) in this duration is given as the difference of two times as both of them are in ‘a.m.’ But before we do that, we need to change 7:30 a.m. completely into hours.
Now, we know that 7:30 is half past 7. That means half an hour has passed after 7 at 7:30.
Thus, we can write 7:30 as:
$7:30=7\dfrac{1}{2}$
Thus, the time between the given time duration is:
$\left( 8-7\dfrac{1}{2} \right)hours$
Now, we know that $7\dfrac{1}{2}=\dfrac{15}{2}$
Thus, we get the time as:
$\begin{align}
& \left( 8-7\dfrac{1}{2} \right)hours \\
& \Rightarrow \left( 8-\dfrac{15}{2} \right)hours \\
& \Rightarrow \left( \dfrac{16-15}{2} \right)hours \\
& \Rightarrow \dfrac{1}{2}hours \\
\end{align}$
Hence, the given time duration is $\dfrac{1}{2}$ hours.
Now, we know that the speed ‘v’ is given as:
$v=\dfrac{s}{t}$ …..(i)
Where, t=time taken
s=distance covered in t time.
We know that here we have:
v=40km/hr
t=$\dfrac{1}{2}$ hour
Now, if we put the values of t and v in equation (i), we will get the value of s.
Thus, putting these values in equation (i) we get:
$\begin{align}
& v=\dfrac{s}{t} \\
& \Rightarrow 40=\dfrac{s}{\dfrac{1}{2}} \\
& \Rightarrow s=40\times \dfrac{1}{2} \\
& \therefore s=20km \\
\end{align}$
Hence, the distance covered in the given duration of time is 20km.
Thus, option (A) is the correct option.
Note:
We here can also obtain the required distance covered by reading the graphs follows:
The given graph is:

Now, if we read the graph, we can see that the car has already covered a distance of 100 km till 7:30 am.
Similarly, we can also read from the graph that the car has covered a total distance of 120km till 8am.
Hence, the distance covered in the given time duration will be the difference between the total distances that have been covered at the starting and the end points of the given duration.
Thus, the required distance is given as:
$\begin{align}
& 120-100 \\
& \therefore 20km \\
\end{align}$
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Business Studies: Engaging Questions & Answers for Success

Trending doubts
Which are the Top 10 Largest Countries of the World?

What are the major means of transport Explain each class 12 social science CBSE

Draw a labelled sketch of the human eye class 12 physics CBSE

Why cannot DNA pass through cell membranes class 12 biology CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

Draw a neat and well labeled diagram of TS of ovary class 12 biology CBSE




