Question

Do the interior angles of a parallelogram sometimes , always or never sum up to $$360$$ degrees?

Answer 1

Hint: In this question, we need to tell whether the interior angles of a parallelogram sometimes , always or never sum up to $$360$$ degrees. Geometrically , there are four interior angles in the parallelogram. First let us know the concept and the definition of the parallelogram. Also by using the concept that all the angles of a parallelogram add up to $$360$$ degree , we can tell whether the interior angles of a parallelogram sometimes , always or never sum up to $$360$$ degrees.

Complete step-by-step answer:
Now, let us know the concept and the definition of the parallelogram.
Parallelogram :
A Parallelogram is nothing but a quadrilateral whose two sides are parallel to each other and all the four angles at the vertices are not $$90$$ degrees or right angles and also The opposite sides of parallelogram are also equal in length.
Now let us see some of the properties of the parallelogram.
A quadrilateral , which has a pair of parallel opposite sides, then it’s a special polygon, and it is known as the Parallelogram.
1. The opposite sides of the parallelogram are parallel and congruent.
2. The opposite angles of the parallelogram are congruent
3. The consecutive angles of the parallelogram are supplementary in nature.
4. If any one of the angles of the parallelogram is a right angle, then all the other angles of the parallelogram will also be at right angle.
5. The two diagonals of the parallelogram bisect each other.
6. Each diagonal of the parallelogram bisects the parallelogram into two congruent triangles.

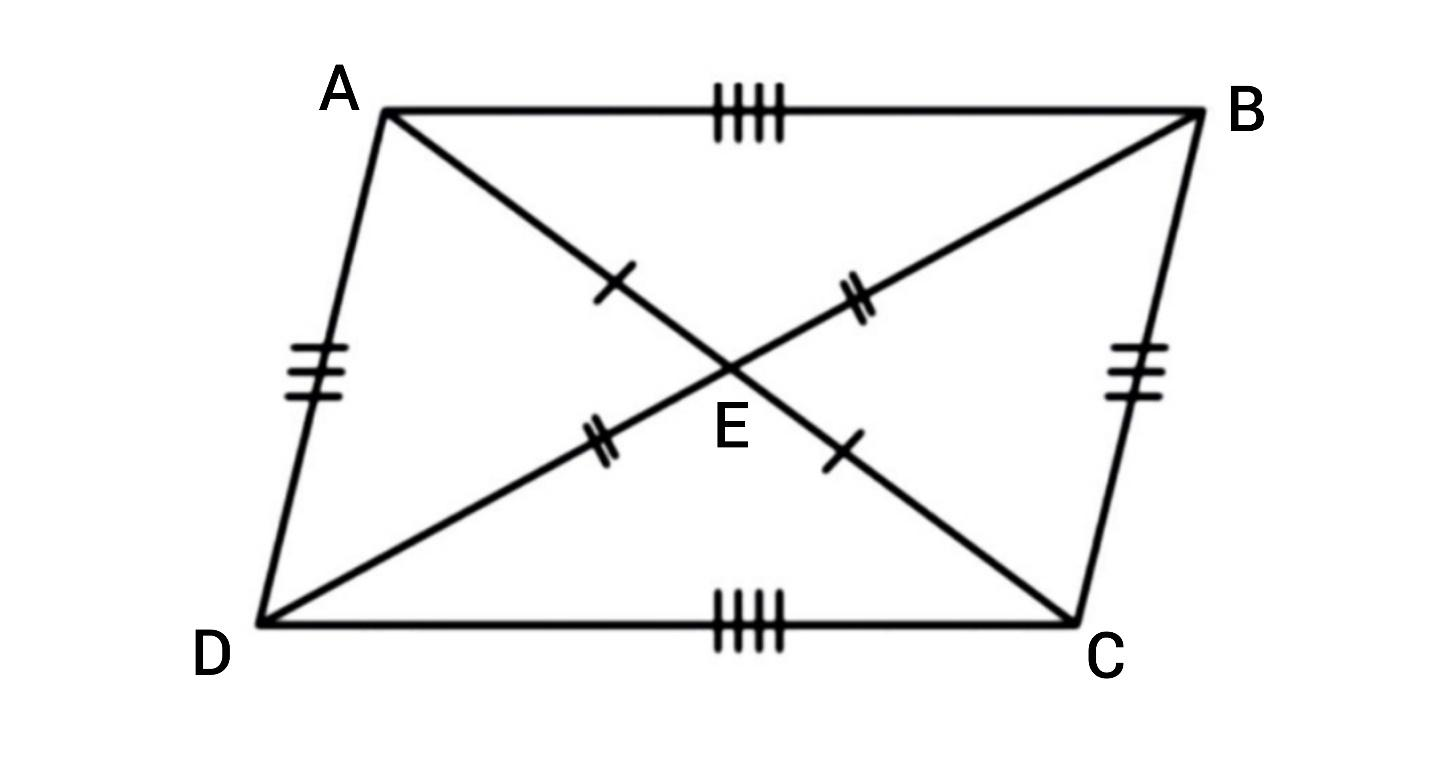
Mathematically, the parallelogram has equivalent opposite interior angles. And also the sum of all four interior angles is always equal to $$360$$ degrees.
Thus we can conclude that the sum of the interior angles of a parallelogram is always $$360$$ degrees.
Final answer :
The sum of the interior angles of a parallelogram is always $$360$$ degrees.

Note: In order to solve these types of questions, we must have a strong grip over the properties of the parallelogram. We also need to know that since the opposite sides of the parallelogram are parallel to each other, and also the diagonals of the parallelogram bisect each other, square is a parallelogram and also the opposite sides of the parallelogram are parallel and diagonals bisect each other, rectangle is also a parallelogram.