Question

What does a negative correlation coefficient mean about a scatter plot of the data?

Answer 1

Hint: We explain this problem using the definition and formula of correlation coefficient by taking the example. We use the definition of scatter plot which is given as the set of points in a coordinate system that do not form any graph known. Also we use the definition of correlation coefficient which gives the relation between to two variables in Cartesian plane and the formula is given as,
\[r=\dfrac{n\left( \sum{xy} \right)-\left( \sum{x} \right)\left( \sum{y} \right)}{\sqrt{\left[ n\sum{{{x}^{2}}}-{{\left( \sum{x} \right)}^{2}} \right]\left[ n\sum{{{y}^{2}}}-{{\left( \sum{y} \right)}^{2}} \right]}}\]
Where, $'n'$ is the number of points in scatter plots.
\['x'\] is the abscissa of points.
$'y'$ is the ordinate of the points.

Complete step by step answer:

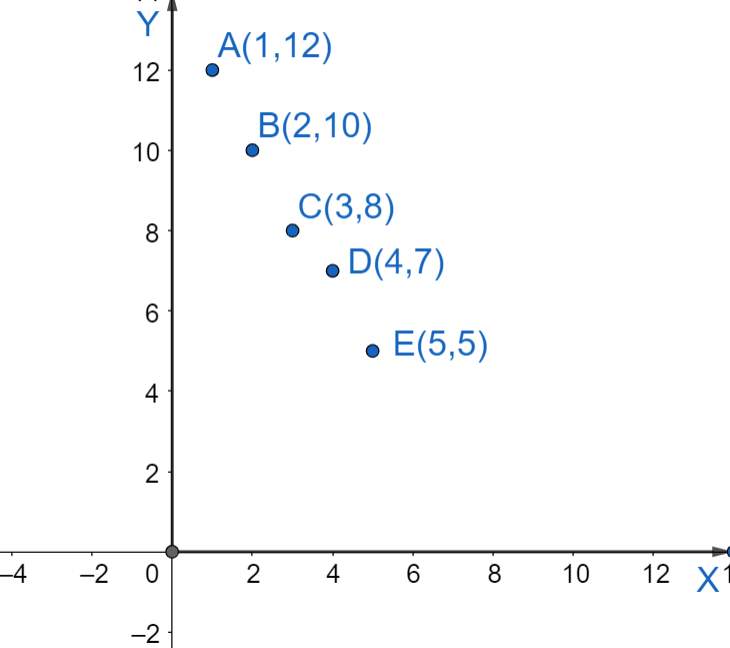
We were asked to explain the negative correlation coefficient of scatter plot.
We know that the scatter plot is defined as the set of points in a coordinate system that do not form any graph known.
Now, let us consider an example of such a scatter plot of 5 points as shown in the above graph.
Here, we can see that the points do not form any specific shape or graph which suggests that above points are scattered in a coordinate plane.
We know that the definition of correlation coefficient which gives the relation between to two variables in Cartesian plane and the formula is given as,
\[r=\dfrac{n\left( \sum{xy} \right)-\left( \sum{x} \right)\left( \sum{y} \right)}{\sqrt{\left[ n\sum{{{x}^{2}}}-{{\left( \sum{x} \right)}^{2}} \right]\left[ n\sum{{{y}^{2}}}-{{\left( \sum{y} \right)}^{2}} \right]}}\]
Where, $'n'$ is the number of points in scatter plots.
\['x'\] is the abscissa of points.
$'y'$ is the ordinate of the points.
Now, let us use this formula for the data we assumed.
Let us find the summation of product of abscissa and ordinate then we get,
$\begin{align}
  & \Rightarrow \sum{xy}=\left( 1\times 12 \right)+\left( 2\times 10 \right)+\left( 3\times 8 \right)+\left( 4\times 7 \right)+\left( 5\times 5 \right) \\
 & \Rightarrow \sum{xy}=12+20+24+28+25 \\
 & \Rightarrow \sum{xy}=109 \\
\end{align}$
Now, let us find the summation of abscissa then we get,
$\begin{align}
  & \Rightarrow \sum{x}=1+2+3+4+5 \\
 & \Rightarrow \sum{x}=15 \\
\end{align}$
Now, let us find the summation of ordinate then we get,
$\begin{align}
  & \Rightarrow \sum{y}=12+10+8+7+5 \\
 & \Rightarrow \sum{y}=42 \\
\end{align}$
Now, by finding the summation of squares of abscissa then we get,
\[\begin{align}
  & \Rightarrow \sum{{{x}^{2}}}={{1}^{2}}+{{2}^{2}}+{{3}^{2}}+{{4}^{2}}+{{5}^{2}} \\
 & \Rightarrow \sum{{{x}^{2}}}=1+4+9+16+25 \\
 & \Rightarrow \sum{{{x}^{2}}}=55 \\
\end{align}\]
Now, by finding the summation of squares of ordinate then we get,
\[\begin{align}
  & \Rightarrow \sum{{{y}^{2}}}={{12}^{2}}+{{10}^{2}}+{{8}^{2}}+{{7}^{2}}+{{5}^{2}} \\
 & \Rightarrow \sum{{{y}^{2}}}=144+100+64+49+25 \\
 & \Rightarrow \sum{{{y}^{2}}}=382 \\
\end{align}\]
Now, let us use these summations in the correlation coefficient formula then we get,
$\begin{align}
  & \Rightarrow r=\dfrac{5\left( 109 \right)-\left( 15\times 42 \right)}{\sqrt{\left( \left( 5\times 55 \right)-{{\left( 15 \right)}^{2}} \right)\left( \left( 5\times 382 \right)-{{\left( 42 \right)}^{2}} \right)}} \\
 & \Rightarrow r=\dfrac{545-630}{\sqrt{\left( 275-225 \right)\left( 1910-1764 \right)}} \\
 & \Rightarrow r=\dfrac{-85}{\sqrt{50\times 146}} \\
\end{align}$
Now, let us simplify the denominator value to its simplest form then we get,
$\Rightarrow r=\dfrac{-85}{2\sqrt{1825}}$
Here, we can see that the correlation coefficient is negative.
Here, we can say that for unit increase in abscissa value the ordinate decreases in the order of $\dfrac{85}{2\sqrt{1825}}$
Therefore, we can conclude that this scatter plot has negative correlation coefficient.
So, we can say that the negative correlation coefficient is obtained when there is an increase in abscissa, the ordinate decreases.

Note: Students may make mistakes by not considering the sign of correlation coefficient. Here, the correlation coefficient is negative which suggests that as abscissa increases the ordinate decreases.
But students take the correlation coefficient to modulus value which will always be positive that gives the wrong result.
So, the correlation coefficient may be positive or may be negative or may be zero also.