Question

What is the domain and range of $y=\sin x$?

Answer 1

Hint: We can define the domain of a function is the complete step of possible values of the independent variable. So, we can say that the domain is the set of all possible ‘x’ values which will make the function ‘work’ and will give the output of ‘y’ as a real number. And the range of a function is the complete set of all possible resulting values of the dependent variable (y, usually), after we have substituted the domain.

Complete step by step solution:
According to our question it is asked of us to calculate the domain and range of $y=\sin x$. For determining the range and domain we have to see the domain and range of sin function. The range of sin functions is defined as $\left[ -1,+1 \right]$ and it is fixed for all sin functions. And the domain of sin function must be between $\left( -\infty ,+\infty \right)$. Both the range and the domain are related to each other. The range of any function decides the values from where to where the function will show and the domain decides the quantity of that graph of the function.

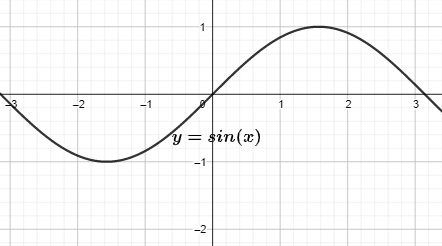
So, if we see in the question then it is clear that it is asked to determine the range and the domain of $\sin x$. So, the range of the fin function always remains the same and that is -1 to +1. Because these functions are varying between ${{1}^{st}}$ and ${{2}^{nd}}$ quadrat always. So, the range is $-1\le y\le 1$, and that can be written as $\left[ -1,+1 \right]$.
The domain of sine function is $-\infty $ to $+\infty $. And this is because the values of a sine function varies between -1 to 1. And it gives the values at $-\infty $ to $+\infty $. So, the domain is $-\infty $ to $+\infty $ and we can write it as $\left( -\infty ,+\infty \right)$.
So, the range of $y=\sin x$ is $\left[ -1,+1 \right]$ and domain is $\left( -\infty ,+\infty \right)$.

Note: We must know the trigonometry concepts to solve this question. The domain where the x value ranges and the range where the y value ranges. Here the function is a form of trigonometric function. So, we have to see the values in which the domain is defined that will be the values of range for this function.