Question

Draw a circle and two lines parallel to a given line such that one is a tangent and the other is a secant to the circle.

Answer 1

Hint: A circle is a round shaped figure that has no corners or edges. In geometry, a circle can be defined as a closed, \[2\]-dimensional curved shape.
A tangent line to a circle is a line that touches the circle at exactly one point, never entering the circle's interior.
In geometry, a secant of a curve is a line that intersects the curve at a minimum of two distinct points. In the case of a circle, a secant will intersect the circle at exactly \[2\] points.
Parallel lines are lines in a plane that are always the same distance apart.
Parallel lines never intersect.

Complete step-by-step answer:

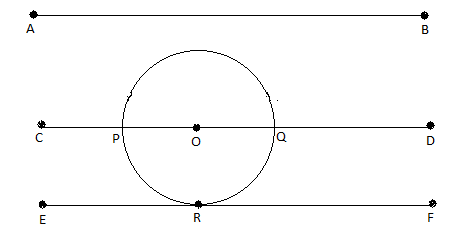
Let the given line be \[AB\]
And circle be with the centre \[O\]
Given, \[AB\parallel CD\parallel EF\]
Here, \[CD\] is a secant. This is because it is interesting the circle at \[2\] points which are \[P\] and \[Q\].
Thus, \[EF\] is a tangent because it touches only \[1\] point at \[R\].
This will be the required image.

Note: It is mandatory that each geometric term and its meaning should be well known by the student. Also the secant \[CD\] can be anywhere inside the circle and it is not necessary that the secant should pass through the centre. The tangent should be drawn in such a way that the line should just touch the circle.
For solving this problem the easiest way is to first draw the secant of the circle followed by drawing the tangent to avoid mistakes and the student can also be able to easily draw the tangent that is parallel to the secant.