Question

Draw a circle with diameter: $ 6cm $ . In each case, measure the length of the radius of the circle drawn.

Answer 1

Hint: As per the given question we have to draw the circle with the given diameter. We know that a circle is a two dimensional figure formed by a set of all those points which are equidistant from a fixed point in the same plane. That fixed point is called the centre of the circle while the fixed distance from the centre of the circle is called the radius of the circle. And we know that the line that passes through the centre and touches the circumference on both sides of the circle is called the diameter.

Complete step by step solution:
In the given question we have the diameter which is $ 6cm $ . Let us assume the $ AB $ is the diameter of the circle so, $ AB = 6cm $ and $ O $ is the centre of the circle.
We know the relation between the radius and the diameter which is diameter is always twice the radius i.e. $ diameter = 2 \times radius $ or we can also write it as
 $ radius = \dfrac{{diameter}}{2} $ . Here radius $ OA = \dfrac{{AB}}{2} $ , it gives us $ OA = \dfrac{6}{2} = 3cm $ .
Also we know that all the radii are equal since they are equidistant from the centre of the circle, so $ OA = OB = 3cm $ . Now taking the radius of the circle and putting the compass at the centre of the circle we will draw the circle around it taking the radius $ 3cm $ .

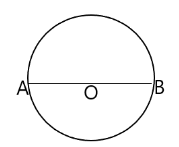
Here in the diagram we can see that $ AB $ is the diameter of $ 6cm $ while $ OA $ and $ OB $ are the radius of $ 3cm $ .
Hence the length of the radius of the circle drawn is $ 3cm $ .

Note: In this type of question we should remember the definition of radius and diameter of the circle and also the relation between them. After this we have to draw the diagram of the circle indicating the radius and centre of the circle. We should also be aware while using the instruments like compass to draw the circle and it should be equal only to the radius of the circle not the diameter.